Why This Paper?
이번에는 Generalized Planning(GP) 문제로 변환하는 접근법이다.
Introduction
추상적 시각 추론 과제(Abstract Visual Reasoning Tasks)는 기계 지능을 이해하고 측정하는 데 사용되어 왔다. 이 중 Abstraction and Reasoning Corpus(ARC)는 Chollet(2019)에 의해 도입된 대표적인 벤치마크로, 여전히 해결되지 않은 도전 과제로 남아 있다.
ARC 문제는 객체 인식(objectness), 목표 지향성(goal-directedness), 위상학(topology), 기하학(geometry) 등의 핵심적인 사전 지식(priors)을 바탕으로 입력과 출력 사이의 규칙을 추론하는 능력을 요구한다. 특히, 일반적으로 3개의 입력-출력 쌍만을 훈련 데이터로 제공하며, 하나 또는 여러 개의 테스트 쌍을 기반으로 일반화해야 하므로 머신러닝 기반 모델이 학습하기 어렵다.

Chollet(2019)는 ARC 문제를 해결하기 위한 방법으로 인간과 유사한 추론을 수행하는 도메인 특화 언어(DSL)의 활용을 제안했다. 하지만, DSL 기반 접근법을 성공적으로 구현한 사례는 많지 않다. 몇몇 연구가 있었지만 DSL의 표현력 부족으로 인해 Kaggle 1위 솔루션보다 성능이 낮았다. Kaggle 1위 솔루션은 방향 비순환 그래프(DAG, Directed Acyclic Graph)를 활용하여 프로그램을 합성하는 방식을 채택했다.
한편 일반화된 계획(Generalized Planning, GP)은 여러 개의 문제를 해결할 수 있는 범용적인 해결책(generalized solution)을 생성하는 프로그램 합성(program synthesis) 접근법으로, ARC 문제 해결에 적합한 방식으로 여겨진다.
본 연구에서는 GP를 기반으로 한 Generalized Planning for Abstract Reasoning(GPAR)을 제안한다. GPAR은 각 ARC 문제를 일반화된 계획 문제로 모델링하고, 최적의 프로그램을 자동으로 합성하는 방식을 사용한다. 이를 위해 PDDL(Planning Domain Definition Language)을 기반으로 한 새로운 인코딩 방식을 도입하고, ARC에 특화된 도메인 지식을 활용하여 탐색 공간을 줄이는 기법을 적용하였다. 실험 결과, GPAR은 ARC 벤치마크에서 최첨단 성능(state-of-the-art performance)을 달성하였다.
Background
Planning Domain Definition Language(PDDL) 다양한 유형의 계획 문제를 모델링하는데 사용되는 표준 언어. 자동화된 계획 솔버(automated planning solvers)를 활용하여 초기 상태에서 목표 상태로의 변환을 찾을 수 있도록 한다.
- 도메인($\mathcal{D}$)
- 술어(predicates)와 행동(action schemes)을 정의
- 행동(action)에는 사전 조건(preconditions)과 효과(effects)가 포함
- 각 행동의 매개변수(parameters)는 인스턴스화 될 수 있음
- 문제(Instance, $\mathcal{I}$)
- 객체(objects), 초기 상태(initial state), 목표(goal formula)를 정의, 목표는 도달해야 하는 상태 집합을 포함
- 같은 도메인을 공유하는 여러 개의 문제를 만들 수 있음
PDDL은 계획 문제를 이렇게 두 부분으로 나눈다. 계획은 행동들의 시퀀스로 구성되며, 행동을 적용하기 위해서는 해당 상태에서 사전 조건(preconditions)이 충족되어야 한다. 결과 상태(resulting state)는 해당 행동의 효과를 반영하여 업데이트 된다. 일반적으로 사전 조건과 효과는 1차 논리(first-order logic)으로 표현되지만 특정한 효과는 더 복잡한 수치 연산(numeric operations)이 필요할 수 있으며, 이를 위해 대체 언어나 시뮬레이터를 사용하는 것이 적절할 수 있다.
이 연구에서는 PDDL을 외부 함수(external functions)와 결합하여 사용하며 명령형 언어(imperative languages)를 활용해 특정 ARC 과제의 복잡한 사전 조건 및 효과를 표현한다.

그림 2는 ARC 과제의 일부를 PDDL 도메인 파일과 인스턴스 파일로 표현한 예시를 보여준다. 행동 스키마(action scheme)와 술어(predicate)의 매개변수는 ? 기호로 표시되고 외부 함수는 @ 기호로 표시된다.
일반화된 계획(Generalized Planning, GP) GP는 같은 도메인 $\mathcal{D}$ 내에서 주어진 유한 개의 계획 문제 $\mathcal{P}$를 해결하는 것을 목표로 한다. 각 인스턴스 $\mathcal{I}$는 초기 상태 $I$, 목표 조건 $G$, 객체 $\Delta$가 다를 수 있다. GP의 해결책은 싱글 프로그램(single program)이며 각 고전 계획 문제에 대해 유효한 계획을 생성할 수 있어야 한다.
포인터 기반 계획 프로그램(Planning Programs with Pointers) 포인터를 사용하는 계획 프로그램은 객체 유형 집합 $\mathcal{P}$에서 포인터 $Z$가 하나의 객체 유형을 가리키도록 하여 GP에서 확장 가능한 솔루션 공간을 컴팩트하게 표현하는 방식이다. 계획 프로그램 $\Pi$는 프로그래밍 가능한 명령어들의 시퀀스이며 아래와 같이 표현된다.
$$\Pi = <w_0,...,w_{n-1}>$$
각 명령어 $w_i$는 다음 중 하나일 수 있다.
- 계획 행동(Planning Action) : 행동 스키마에서 가져온 행동을 실행, 포인터나 상수 객체 참조 가능
- RAM 액션(RAM Action) : 포인터를 조작하는 명령어
- 테스트 액션(test action) : 술어(predicate)의 해석을 담당하는 명령어
- 이동 명령어(goto action) : 비순차적 실행을 위한 명령어로 goto$(i',y_z)$의 형식을 가진다. $i'$은 이동할 프로그램의 라인(destination line)이고 $y_z$는 RAM 액션 또는 테스트 액션의 마지막 실행 결과를 반영하는 논리적 명제이다.
- 종료 명령어(end Instruction) : 항상 프로그램의 마지막 줄에 있으며, 실행을 종료한다.
그림 3의 상단은 GP 솔버가 실행하는 계획 프로그램이 크기 1의 노드의 색상을 검정으로 변경하는 방식을 보여준다. 두 개의 포인터(no: 노드 객체를 가리킴, co: 색상 객체를 가리킴)를 사용한다.

라인 0~4에서는 노드의 색을 변경하는 UpdateColor 행동을 실행하며 no의 값을 증가시켜 다음 노드를 가리킨다. 만약 마지막 노드 객체를 가리켜 포인터 증가가 실패할 경우 라인 5~7로 넘어간다. 5~7에서는 no가 다시 첫 번째 노드로 설정되고 co의 값을 늘려 다음 색상을 가리키도록 업데이트한다. 결국 모든 색상이 시도되면 프로그램이 종료된다.
Abstraction over ARC
추상화(Abstraction)은 GPAR에서 객체 인식을 가능하게 하여 개별 픽셀이 아니라 픽셀 그룹을 한 번에 수정할 수 있도록 하여 검색 공간(search space)을 축소하는 역할을 한다. ARC를 해결하는 인간은 객체 간의 관계를 활용하는 방식으로 해결책을 도출하는 경향이 있다. 그러나 이미지 해석 방식이 다양하기 때문에 다른 문제에서는 다른 "객체" 정의가 필요할 수 있다.
우리는 ARC 문제에 대응하기 위해 8가지의 추상화 방식을 고려한다.
- 4-연결(4-connected) : 배경을 제외하고 4-연결된 픽셀 집합을 하나의 노드로 간주함
- 8-연결(8-connected) : 배경을 제외하고 8-연결된 픽셀 집합을 하나의 노드로 간주함
- 동일 색상(Same-color) : 연결성과 무관하게 같은 색상의 모든 픽셀을 하나의 노드로 처리함
- 다중 색상(Multi-color) : 배경을 제외한 모든 색상을 동일하게 취급하여 4-연결 및 8-연결된 컴포넌트로 노드를 형성함
- 수직 및 수평(Vertical and Horizontal) : 배경을 제외하고 동일한 색상의 픽셀을 기준으로 세로 또는 가로 방향으로 노드를 형성함
- 픽셀 기반(Pixels) : 각 픽셀을 개별적인 노드로 취급함
- 이미지 기반(Image) : 전체 이미지를 단일 노드로 간주함
- 최대 직사각형(Max-rectangle) : 4-연결된 컴포넌트 내부에서 최대 크기의 직사각형을 찾아 이를 하나의 노드로 설정

특정 추상화 방식만이 유효한 경우가 있다. 그림 4(왼쪽)에서는 4-연결 추상화만 적절하다. 그러나 그림 4(오른쪽)처럼 2가지 추상화 방식이 동일한 결과를 나타낼 수도 있다. 중복을 피하기 위해 적어도 하나의 인스턴스에서 크기, 색상, 형태가 다른 노드 표현을 생성하는 경우에만 고려한다.
노드 속성(Node Attributes) 각 식별된 노드는 색상, 크기, 형태와 같은 요소를 포함한다. 형태는 단일 픽셀, 정사각형, 직사각형, 가로선, 세로선, 왼쪽 대각선, 오른쪽 대각선, 혹은 미확정(unknown)이다.
객체 개수 및 정렬 관련 속성
- 객체 개수나 정렬 관련 작업을 해결하기 위함
- 가장 크거나 작은 크기의 노드
- 홀수 또는 짝수 크기의 노드
- 가장 많이 또는 가장 적게 나타나는 색상의 노드
추상화 방식에 따른 속성 조정
- 일부 추상화 방식에서는 대체 속성을 사용
- 다중 색상 노드에서는 색상 속성(color attribute)이 생략
- 픽셀 노드 및 이미지 노드를 고려할 때는 가장 많이/적게 등장한 색만 식별
픽셀 노드(Pixel Nodes) 추가 속성
- 이미지 기하학적 구조를 반영하는 추가 속성을 포함
- 이미지 경계(border)
- 중심 대각선(centric-diagonal)
- 수직 중앙선(middle-vertical line)
- 수평 중앙선(middle-horizontal line)
- 노이즈 제거를 위해 크기가 1픽셀인 4-연결 컴포넌트 제거
노드 간 관계(Relations between Nodes) 우리는 3가지 유형의 노드 관계를 정의하며 이는 픽셀 노드 및 이미지 노드를 제외한 모든 노드 정의에 적용 가능하다.
- 공간적 관계(Spatial Relations)
- 두 노드가 상하좌우 관계 : 각 노드에 적어도 하나의 픽셀 존재, 동일한 축에서 같은 좌표 값을 가져야함
- 대각선 관계 : 두 노드의 형태가 알려져 있으며(unknown이 아님), 각 노드의 꼭짓점이 동일한 대각선 축에서 정렬
- 합동 관계(Congruent Relations)
- 형태와 크기가 동일한 노드들 간의 관계
- 색상이 같은 노드들도 합동 관계를 가질 수 있음
- 포함 관계(Inclusive Relations)
- 특정 노드가 다른 노드를 포함하거나 부분적으로 포함하는 관계
- 완전 포함(contains) : 포함된 노드의 모든 픽셀이 포함하는 노드의 경계(border) 내에 있음
- 부분 포함(partially contains) : 포함된 노드의 경계가 이미지의 경계를 터치하는 경우
노드의 속성과 관계는 핵심 사전 지식(core knowledge priors)에 기반하여 정의되며 이를 표준 이미지 처리 기법을 통해 추출한다.
Domain-Specific Language
PDDL은 1차 논리(First-Order Logic)의 일부를 활용하여 객체 간 관계 및 속성을 구조적으로 표현한다. PDDL에서는 각 ARC 문제를 단일 도메인 파일과 유한 개의 인스턴스 파일로 표현한다.
- 도메인 파일
- 노드 간 관계 및 속성을 술어(predicate)로 모델링
- 노드 변환을 행동 스키마(action schemes)로 표현
- 인스턴스 파일
- 초기 상태(initial state) : 입력 이미지를 표현하는 술어
- 목표 상태(goal state) : 출력 이미지를 표현하는 술어
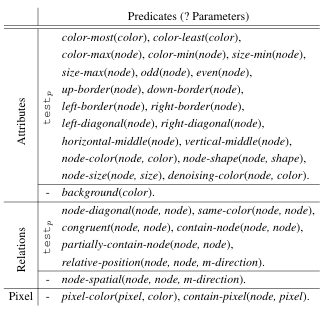
표 1은 사용 가능한 객체와 유형을 정리한 것이고 표 2는 노드 속성과 관계를 모델링하는 술어(predicate) 목록을 정리한 것이다. 그리고 표 3은 DSL(Domain-Specific Language)에서 사용되는 주요 행동 스키마(action schemes) 목록이다.


행동에서는 저수준 행동과 고수준 행동을 혼합하여 표현하며, 일부 고수준 행동은 복잡한 변환을 인코딩하여 저수준 행동만으로 구현했을 때 필요한 프로그램 라인 수를 줄여준다. 예를 들어 SwapColor와 CopyColor는 저수준 행동인 UpdateColor로 구현이 가능하지만 매우 많은 프로그램 라인이 필요하다.
각 추상화 방식은 고유한 행동과 술어 집합을 가진다. 또한 복잡한 이동, 확장, 및 합동 노드 연산을 수행하기 위한 2가지 추가적인 추상화 방식을 고려한다. 이 방식은 4-연결 추상화와 동일한 노드 정의를 사용하며 더 간단한 추상화 방식으로 해결책을 찾지 못할 경우에만 적용된다.
행동 가지치기(Action Pruning) 추상화가 항상 옳은 것은 아니다. 때로는 추상화가 불필요한 행동(irrelevant actions)을 초래할 수 있다. 예를 들어 그림 1의 첫 번째 문제에서는 노드의 위치를 변경하는 행동이 필요하지 않다. Xu, Khalil, and Sanner(2023)에서도 유사한 개념을 논의했으며 가지치기하는 방법을 제안했다. GPAR은 노드 자체를 가지치기하는 것이 아니라 도메인 파일을 생성할 때 불필요한 행동 스키마를 사전에 제거한다.
GPAR은 훈련 데이터에서 입력과 출력 이미지 간 변화가 없는 속성을 기준으로 행동을 가지치기한다. 예를 들어 모든 노드의 위치, 색상, 크기가 변하지 않는 경우에는 관련된 행동(이동, 색상 변경, 크기 조정)을 가지치기한다. 또한 특정 추상화 방식에서 적용할 수 없는 행동도 추가적으로 가지치기를 진행한다.
Program Synthesis
우리는 PGP(v) 솔버를 활용하고 개선하여 ARC 문제의 훈련 인스턴스에 대한 계획 프로그램을 탐색한다. 솔버가 모든 훈련 인스턴스를 해결하는 프로그램을 생성하면, 해당 프로그램을 이용하여 테스트 인스턴스에서 솔루션을 평가한다.
솔버의 핵심 엔진은 휴리스틱 탐색 알고리즘이며, 빈 프로그램에서 시작하여 한 줄씩 명령어를 추가하면서 해결책을 찾을 때까지 탐색을 진행한다.
술어 제약과 인자 제약(Predicate and Argument Constraints)
- 술어 제약(Predicate Constraints)
- 탐색 시작 전에 결정하여 불필요한 액션이 포함되지 않도록 함
- 해석할 수 있는 술어(predicate)의 인자(arguments)를 제한하는 규칙
- 모든 이미지의 노드가 동일한 속성을 가지면 해당 속성을 조건으로 사용하는 것은 의미 없음
- 인자 제약(Argument Constraints)
- 테스트 액션에서 사용되는 인자가 모든 훈련 및 테스트 입력 이미지에서 존재하는 속성을 참조하도록 보장
- 특정 입력 데이터에 과적합되는 것을 방지
- ex) 그림 1의 두 번째 그림을 보면 트레이닝과 테스트의 입력 개수가 다르다
구조적 제한(Structural Restrictions) 구조적 제한은 탐색 공간에서 대칭을 줄이기 위한 전략으로 사용된다. 우리는 계획 프로그램을 적용 섹션과 반복 섹션으로 나눠서 구조적 제한을 적용한다.
- 적용 섹션(Application Section)
- 계획 행동, 테스트, goto 명령어 포함 가능
- 탐색 중에 탐색 알고리즘이 작성하는 부분
- 제약 조건:
- 테스트 액션은 반드시 goto 명령에 뒤에 와야 한다
- 첫 번째 줄은 반드시 테스트 액션으로 시작해야 한다
- DSL의 행동이 한 번 등장하면, 그 이후에는 DSL 행동이 연속으로 등장하거나 반복 섹션이 이어져야 함
- 반복 섹션(Looping Section)
- 포인터를 조작하는 명령어 및 goto 명령어의 연속적인 실행을 포함
- 모든 가능한 포인터 값 조합을 순회(iterate)하도록 설계
- 마지막에는 end 명령어가 포함

그림 5는 복잡한 논리를 포함한 계획 프로그램(planning program)의 실행 과정을 보여준다.
- 첫 번째 테스트된 속성이 거짓(false)일 때만 ExtendNodeDirection 행동이 실행됨 (라인 0)
- 두 번째 테스트된 공간적 관계(spatial relation)가 참(true)이면 실행됨 (라인 2)
- 총 3개의 포인터를 활용하여 탐색함
휴리스틱 함수(Heuristic Function) 픽셀 관련 술어를 활용하여 픽셀 정보를 탐색을 안내하는 기준으로 사용한다. 새로운 프로그램이 생성될 때마다 이를 실행하여 휴리스틱 함수 $h_p$를 적용한다.
휴리스틱 함수 $h_p$는 목표 상태와 현재 상태의 픽셀 차이를 계산하여 초기 상태에서 변경되었지만 아직 목표 상태와 일치하지 않는 픽셀에 대해 추가적인 패널티를 부여한다. 즉, 현재 상태를 목표 상태에 더 가깝게 만드는 프로그램을 우선적으로 탐색하게 유도한다.
탐색 알고리즘은 기본적으로 휴리스틱 함수 $h_p$를 기반으로 방향을 결정한다. 만약 동점이 발생하면 추가적인 휴리스틱 함수 ,$h_{ln}$을 적용하여 DSL에서 정의된 행동을 우선적으로 고려한다.
포인터 기반 부분 인스턴스화(Instantiation over Pointers) GPAR에서는 일부 매개변수를 포인터, 일부는 객체로 대체하는 부분 인스턴스화를 지원한다.필요한 매개변수보다 적은 수의 포인터만 할당되면 일부 매개변수는 직접 객체로 채워지는 방식으로 인스턴스화 된다.
부분 인스턴스화를 사용할 경우 테스트 액션이 특정 속성을 고정하여 루프와 분기를 유연하게 조절할 수 있다.
System Overview

그림 6은 GPAR의 파이프라인 개요를 보여주는 스케치로 DSL Generation 단계와 Program Synthesis 단계로 이루어진다.
- DSL 생성 단계(DSL Generation State)
- 다양한 추상화를 사용하여 도메인 파일과 관련된 인스턴스 파일 생성
- 노드 객체, 속성, 관계 정의를 기반으로 추상화를 수행
- 행동 제약과 중복 제거를 적용
- 중복되지 않는 추상화를 선택
- 프로그램 합성 단계(Program Synthesis Stage)
- 도메인 파일과 인스턴스 파일에 기반하여 실행 가능한 프로그램을 생성
- 행동과 술어를 인스턴스화하여 구체적인 계획 행동과 테스트 액션을 생성
- 각 프로그램 라인에 따라 goto 명령어를 생성하여 프로그램 흐름 구성
- 술어 및 인자 제약(predicate and argument constraints)을 적용
여기서 PGP(v) 솔버는 사용자 입력과 다양한 탐색 매개변수를 활용하여 적용 섹션과 반복 섹션을 프로그래밍한다. 프로그램 라인 수, 포인터 집합, 새로움 임계값(novelty threshold)의 매개변수를 사용한다.
PGP(v)의 결과물은 계획 프로그램 $\Pi$이며 이는 입력 이미지를 목표 이미지로 변환하는 함수 역할을 수행한다. 만약 $\Pi$가 모든 테스트 인스턴스에서 유효한 해결책으로 검증되면 최종적인 해결책으로 채택된다.
Experiments
우리는 Xu, Khalil and Sanner(2023)에서 제시한 객체 중심(object-centric) ARC 문제 160개를 벤치마크로 사용한다. 이런 문제들은 아래와 같이 3가지 유형으로 분류된다.
- 재색칠 문제(Recoloring) : 객체의 색상을 변경하는 문제
- 이동 문제(Movement) : 객체의 위치를 변경하는 문제
- 증강 문제(Augmentation) : 객체의 크기 또는 패턴과 같은 속성을 변경하는 문제
그림 1은 각 유형의 대표적인 예제를 보여준다.
Parameters
PGP(v) 솔버는 아래의 3가지 매개변수를 사용하여 탐색을 수행한다.
- $n$(프로그램 라인 수) : 프로그램에서 허용되는 최대 라인 수(3~10 범위)
- $v$(새로움 임계값) : 특정 행동이 프로그램에서 등장할 수 있는 최대 횟수(1~3 범위)
- $Z$(포인터 집합) : 사용 가능한 포인터의 조합(표 4 참고)
$n$ 값에 따라 $v$의 설정 규칙이 변하게 된다.
- $n = 3$일 때, $v = 1$(각 명령어는 한 번만 등장 가능, 테스트 액션, goto, 계획 행동 1회씩)
- $n = 4$일 때, $v = 1$ 또는 $2$(계획 행동이 최대 2 번 등장 가능)
- $n > 4$일 때, $v$ 값은 1~3 범위에서 설정됨


포인터 $Z$는 액션 스키마에서 일반적으로 사용되는 매개변수기 때문에 NODE, COLOR, M-DIRECTION 객체 유형만 참조한다. 탐색 공간의 복잡도는 $n$과 $v$값에 비례하며 둘의 상한 값을 설정하여 계산 가능하도록 복잡도를 유지한다.
PGP(v)는 각 ARC 문제에 대해 낮은 $n$과 $v$값부터 시작하여 복잡도를 점진적으로 증가시키면서 실행한다. 단순한 추상과가 먼저 고려되며, 각 조합은 1800초 제한 내에 실행되며 처음 발견된 $\Pi$를 솔루션으로 채택하여 테스트 검증을 수행한다.
실험은 Kaggle 챌린지 1위 모델과 ARGA(최신 기법)과 비교를 진행했다. 모두 동일한 1800초 제한을 두고 실행하였으며 Kaggle 1위 모델과 ARGA는 생성된 후보 솔루션 중 최고 점수를 받은 것을 최종 해결책으로 선택했다.
Synthesis of Solutions
표5는 GPAR, ARGA와 Kaggle 챌린지 1위 모델의 훈련 및 테스트 정확도를 비교한 결과를 보여준다.
GPAR은 재색칠(Recolor) 문제에서 다른 모델보다 뛰어난 성능을 보였다. 테스트 정확도에서 모든 접근법을 능가하였고 유일하게 50% 이상의 ARC 문제를 해결했다.(훈련 데이터 : 53.75%, 테스트 데이터 : 50.63%). 그리고 훈련과 테스트 간 정확도 차이가 가장 적어 일반화 성능이 우수하다.
문제의 유형별로 성능을 분석해보면
- 재색칠(Recolor) 문제 : GPAR가 가장 우수한 성능을 보임
- 조건문 기반의 명령형 프로그램으로 효율적으로 해결 가능
- 주로 크기, 모양, 색상과 같은 속성을 기반으로 동작
- 이동(Movement) 문제 : 공간적 관계 표현이 어려움
- 중심, 모서리, 영역 등 동적인 속성을 필요로 하는 문제 해결이 어려움
- 일부 문제는 큰 숫자 값의 이동을 요구하지만 현재 GPAR의 DSL에서는 이를 지원하지 못함
- 증강(Augmentation) 문제 : 모든 플래너가 어려움을 겪음
- 크기 조정, 도형 완성, 유사 복제 등 복잡한 변환이 포함
- DSL 기반 명령형 프로그램에서 구현하기 어려운 유형
- 모든 플래너가 이 범주에서 훈련 및 테스트 정확도가 50% 이하
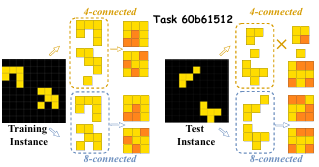
일반화 성능을 분석해보면 GPAR도 훈련과 테스트 간 성능 차이가 존재했다. 그림 7의 예제를 보면 훈련 인스턴스에서는 4-연결과 8-연결 추상화 모두 해결이 가능하지만 테스트에서는 8-연결만이 정답을 생성한다.
GPAR가 해결한 테스트 문제 중 절반 이상은 매우 단순한 해결책을 필요로 한다. 즉 50%이상의 테스트 문제는 $v = 1$이며 프로그램 길이 $n = 3$으로 해결이 가능하다. 다시 말하면 반복되는 행동 없이 단순한 조건과 행동만으로 해결이 가능하다. 81개 중 44개 문제는 하나의 조건만으로 해결이 가능하다.
이러한 결과는 DSL과 PGP(v) 솔버의 효율성을 보여준다. 효율적인 DSL 덕분에 최소한의 행동과 조건만으로 해결이 가능하며 이로 인해 일반화 성능이 높은 결과가 나타난다.
Conclusion
우리는 GP 솔버를 활용하여 포인터 기반 프로그램을 생성하고 ARC 문제에서 최고 성능을 달성했다. PDDL을 이용하여 객체 중심 추상화를 모델링하여 일반화 성능을 향상시켰지만 유용한 추상화를 찾는 것은 여전히 해결되지 않은 과제이다. 향후 연구에서는 새로운 휴리스틱과 대체적 계획 모델을 탐색하여 성능 향상을 목표로 한다.
https://ojs.aaai.org/index.php/AAAI/article/view/29996