메타 강화학습에 대해 공부를 하기 위해 "A Survey of Meta-Reinforcement Learning"이라는 논문을 참고하여 정리를 진행할 예정이다. 분량이 많기에 나눠서 정리를 진행하고자 한다.
Introduction
Meta-reinforcement learning(meta-RL)은 '강화학습을 학습하는' 메타러닝의 한 형태이다. 즉, meta-RL은 샘플효율성이 낮은 ML을 이용하여 샘플 효율성이 높은 RL 알고리즘을 학습하는 것이다. meta-RL은 meta-learning에서도 특별한 경우이며 학습하는 알고리즘이 RL이기 때문이다. Meta-RL은 오랫동안 하나의 머신러닝 문제로 다뤄졌으며 최근 연구에서는 meta-RL과 유사한 작동 방식에 뇌 속에서 관찰되었다는 결과도 있다.
Meta-RL은 기존의 RL의 한계를 넘을 수 있는 잠재력이 있다. deep RL에 대한 방법들이 몇 년 간 발전해왔고, 바둑과 같은 게임, 성층권 풍선 항법, 복잡한 지형의 로봇 보행 등에서 성공을 보였다. RL은 높은 샘플 비효율성을 가지고 있으며 실제 세계에서 적용되기 어려운 한계점을 보유한다. Meta-RL은 현재 존재하는 RL 방법보다 더 효율적인 RL 알고리즘을 생산할 수 있다.
동시에 향상된 샘플 효율성을 만들기 위해서는 두 가지의 비용이 발생한다. 첫 번째는 기존 학습보다 더 많은 양의 데이터를 요구한다는 것이고, 그 이유는 meta-RL이 전체 알고리즘 자체를 학습하기 때문이다. 두 번째는 meta-learning은 meta-training 데이터에 맞춰 학습하기 때문에 다른 데이터에 일반화 능력을 떨어트린다. meta-learning이 제공하는 trade-off는 테스트 시점의 샘플 효율성 향상과 훈련 데이터 요구량 증가 및 테스트 시점의 일반화 성능 저하 사이의 균형이다.
Example application 로봇 셰프가 자동으로 요리하는 작업의 예시가 있다고 해보자. 로봇이 누군가의 부엌에서 일할 때 로봇은 부엌에 적합한 정책을 학습할 것이고 각 부엌은 서로 다른 모양을 가지고 있을 것이다. 이 문제는 요리에 필요한 모든 물건이 눈에 보이지 않는다는 점에서 더 복잡해진다. 냄비는 찬장 속에, 향신료는 높은 선반 위에 숨겨져 있을 수 있다. 따라서 로봇은 부엌의 전반적인 구조를 이해할 뿐 아니라 특정 물건의 위치를 발견하면 그것을 기억해야 한다.
새로운 부엌에서 로봇을 처음부터 학습시키는 것은 초기에 무작위 행동을 하므로 위험할 가능성이 있다. 하나의 대안은 단일 부엌에서 사전 학습을 진행하고 새로운 부엌에서 fine-tuning을 진행하는 것이다. 그러나 이 방식은 이후 fine-tuning 과정 자체에 대한 고려가 부족하다.
대조적으로 meta-RL에서는 다양한 훈련용 부엌 분포에 대해 로봇을 훈련시켜 새로운 부엌에도 쉽게 적응할 수 있도록 만든다. 이런 방식으로 로봇을 학습시키는 것이 모인 데이터를활용하는 것과 데이터를 수집하는 것에서 더 좋은 성능을 보인다. meta-RL은 더 많은 샘플을 요구하지만 한 번만 수행하면 되며, 결국 새로운 부엌에서 일할 때 더 높은 샘플 효율성을 보여준다.
이 예시가 보여주는 것은 meta-RL이 효율적인 적응이 자주 요구되는 상황에서 특히 유용하다는 점을 보여준다. 이런 경우 초기 meta-training 비용이 상대적으로 작게 느껴질 수 있다. 많은 경우, 비효율적인 샘플 학습에 미리 대규모로 투자하는 것은 추후 적응력을 개선하기 위해 가치있는 일이다. 이러한 예시는 meta-RL이 지향하는 이상적인 응용 사례를 보여주며, 실제로 로봇 조작이나 로봇 보행 등과 같은 보다 제한적인 로보틱스 과제들에 meta-RL이 적용되고 있다.
Survey scope 조사 범위는 meta-RL이 머신러닝 주제로 다룬 연구에 초점을 맞추며 다른 분야의 연구는 제외했다. meta-RL이 머신러닝에 적용된 폭과 깊이를 알기 위해 주요 머신러닝 컨퍼런스들을 조사했고 2017년부터 2022년 사이를 조사했다. meta-RL 연구는 2016년 이후 활발히 등장하기 시작했으며, 대부분의 주요 연구는 NeuralIPS, ICML, ICLR에 집중되어 있었다. 우리의 조사가 이런 컨퍼런스와 시기를 중심으로 이뤄졌지만 범위를 벗어난 관련된 논문도 다룬다. meta-RL을 명시적으로 언급하지 않아도 주제에 부합하다고 판단되는 논문이면 포함시켰다. 마지막으로 우리의 조사는 meta-RL 연구의 모든 연구를 포괄하려는 시도는 아니며, 핵심적이고 중요한 아이디어와 연구 방향에 대한 개요를 제시하는게 목적이다.
survey overview 본 조사의 주요 목적은 meta-RL에 대한 입문 지점을 제공하고 해당 분야의 현재 연구 현황과 미해결 과제를 조망하는 것이다.
Background 파트에서는 meta-RL을 정의하고 어떤 문제에 적용이 가능한지 예시와 함께 볼 것이다.
Few-Shot Meta-RL 파트에서는 meta-RL에서 가장 많이 발생하는 few-shot meta-RL을 볼 것이다. 여기서 목표는 빠르게 적응하는 RL 알고리즘을 학습하는 것이다. 이런 알고리즘은 특정 작업 분포가 주어졌을 때 해당 분포 내의 새로운 작업에 효율적으로 적응할 수 있도록 메타 학습된다. 그림 1에서 장난감으로 이런 예시를 표현한 것을 볼 수 있다. 여기서 agent는 2D 평면에서 목표 지점에 가는 것을 학습하는 방법을 메타 학습한다. 이런 agent는 보지 못한 목표지점에도 효율적으로 적응할 수 있을 것이다.

Many-Shot Meta-RL 파트에서는 many-shot 설정을 고려할 것이다. 여기서 목표는 좁은 작업 분포에 국한되지 않는 범용 RL 알고리즘을 학습하는 것입니다. 여기에는 두 가지 접근 방식이 있는데 여러 작업 분포에 기반한 학습 또는 단일 작업에 대해 표준 RL 학습과 함께 메타 학습을 병행하는 방식이 있다.
Application 파트에서는 로보틱스와 같은 분야에서 meta-RL이 실제로 적용되는 예시를 볼 것이다. 그 후 연구의 문제점을 Open Problems 파트에 기술할 것이다. 여기에는 few-shot meta-RL의 일반화 문제, many-shot meta-RL의 최적화 문제, meta-training 비용 절감 등의 과제가 포함된다.
Background
meta-RL은 RL 알고리즘으로 넓게 표현이 가능하다. 여기서는 meta-RL의 정의와 공식을 소개할 것이다. 그러기 위해 먼저 RL이 뭔지 정의하는 것부터 시작하자.
Reinforcement Learning
RL 알고리즘은 Markov decision process로 부터 action을 진행하는 policy를 학습하는 것이다. MDP는 튜플 $\mathcal{M} = \langle \mathcal{S}, \mathcal{A}, P, P_0, R, \gamma, T \rangle$로 정의되며
- $\mathcal{S}$ : state의 집합
- $\mathcal{A}$ : action의 집합
- $P(s_{t+1}\mid s_t,a_t)$ : state $s_t$에서 action $a_t$를 적용했을 때 state $s_{t+1}$로 전이 될 확률
- $P_0(s_0)$ : 초기 상태에 대한 분포
- $R(s_t,a_t)$ : 보상 함수
- $\gamma$ : 할인 계수(discount factor)
- $\pi(a\mid s)$ : state에서 action을 진행할 확률 분포를 매핑한 함수
- $T$ : 에피소드 길이
단순화를 위해 유한한 horizon을 가정하여 정의를 내렸지만 실제 많은 알고리즘은 무한한 설정에서도 작동한다. MDP와 policy의 상호작용은 에피소드 단위로 진행되며 $P_0$에서 시작해 policy $\pi$와 dynamics $P$를 이용하여 action을 샘플링 한다. $T$ 번 끝났을 때 새로운 에피소드가 시작되며 각 전이마다 보상은 $r_t = R(s_t, a_t)$로 정의된다. 이것을 에피소드의 확률 분포에 대해 정의하면:
$$P(\tau) = P_0(s_0)\prod_{t=0}^{T}\pi(a_t\mid s_t)P(s_{t+1}\mid s_t,a_t)$$
때때로 우리는 데이터 $\tau = \{s_t, a_t, r_t, s_{t+1}\}^T_{t=0}$로 구성된 데이터를 trajectory라고 부른다. RL의 목적은 에피소드를 진행하며 누적 보상을 최대화 하는 policy를 학습하는 것이다:
$$J(\pi) = \mathbb{E}_{\tau \sim P(\tau)}\left [ \sum_{t=0}^{T}\gamma^tr_t \right ]$$
여기서 $r_t$는 trajectory $\tau$를 통해 얻은 보상이다. 최적화하는 과정에서 다양한 에피소드가 수집된다. 만약 $H$개의 에피소드가 모아졌다면 $\mathcal{D} = \{\tau^h\}^H_{h=0}$의 데이터가 MDP 안에 수집된다. RL 알고리즘은 데이터를 policy에 매핑하는 함수이다. 학습 과정 중 데이터를 수집하기 위해 사용하는 중간 policy는 필수적으로 그리디한 선택을 하지 않고 대신 탐색을 포함할 수 있다. 본 조사에서는 파라미터화된 정책을 다루며, 이 파라미터는 $\phi \in \Phi$로 표기한다. 따라서 우리는 RL 알고리즘을 $f(\mathcal{D}) : ((\mathcal{S} \times \mathcal{A} \times \mathbb{R})^T)^H \to \Phi$라고 정의했다.
Meta-RL definition
RL 알고리즘은 전통적으로 사람에 의해 설계되고 평가되었다. meta-RL의 아이디어는 RL 알고리즘의 일부를 머신러닝을 통해 직접 학습하는 것이다. 다시 말해, RL이 policy를 학습할 때 meta-RL은 policy를 배출하는 알고리즘 $f$를 학습한다는 뜻이다. 이것은 과정에서 사람의 손길을 전부 지우지는 못하지만 RL 알고리즘을 설계하는 과정을 훈련된 환경과 파라미터들에게 옮길 수 있다.
이러한 2단계 구조에서 $f$를 학습하는 알고리즘은 outer-loop로, $f$를 학습하는 것은 inner-loop로 불린다. inner-loop와 outer-loop 간의 관계는 그림 2에서 확인이 가능하다. 둘 다 학습으로 취급되지만 inner-loop는 적응력, outer-loop는 메타 학습을 나타낸다. 학습된 $f$는 meta-testing 과정에서 평가된다. 우리는 메타 학습하는 RL 알고리즘 혹은 새로운 MDP에 빠르게 적응하는 inner-loop를 원한다. 이를 위해서는 여러 개의 훈련용 MDP들에 접근할 수 있으어 하며 이들은 작업 분포 $p(\mathcal{M})$로부터 샘플링된다.
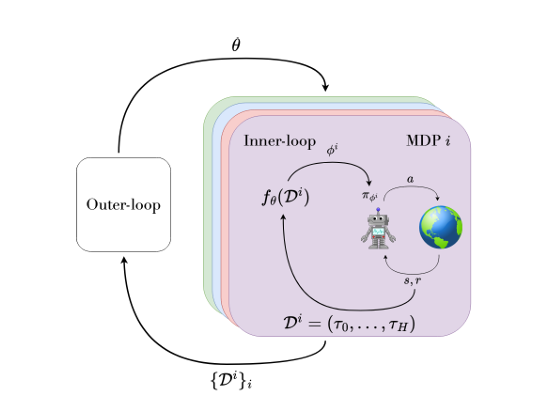
이론적으로는 어떤 종류의 작업 집합도 사용 가능하지만 실제로는 공통된 $\mathcal{S}$와 $\mathcal{A}$는 모든 task 간 공유되는 반면, 보상 함수 $R(s,a)$와 전이 확률 $P(s'\mid s,a)$와 시작 분포 $P_0(s_0)$만 서로 다르게 설정되는 경우가 많다.
메타 학습 과정은 작업 분포로부터 task를 샘플링하고 해당 task에 대해 inner-loop를 돌면서 policy들을 향상하는 알고리즘을 최적화 한다. 작업과 inner-loop가 상호작용 하는 것을 lifetime 혹은 trial이라고 부르며 그림 3에서 확인이 가능하다. trial은 다양한 에피소드들로 구성될 수 있고, 각 에피소드가 끝나면 새로운 에피소드는 초기 상태 분포로부터 시작된다.

Parameterization 우리는 일반적으로 inner-loop를 meta-파라미터 $\theta$를 가진 함수 $f_\theta$로 파라미터화하며 이 파라미터를 통해 meta-RL을 최대화하는 것을 학습한다. $f_\theta$는 policy의 파라미터 $\phi$를 직접 출력하며 이 관계는 $\phi = f_\theta(\mathcal{D})$로 표현이 가능하다. 우리는 policy $\pi_\phi$를 기본 policy라고 부른다.
일반적으로 policy 파라미터 중 일부는 inner-loop에서 task에 맞춰 적응하고 나머지 일부는 outer-loop에서만 메타 업데이트 된다. 이를 구분하여 $\pi_{\phi,\theta}$와 같이 나타낸다. 이때, inner-loop에 적응하는 policy 파라미터를 adapted policy parameters 혹은 task parameter라고 부른다.
여기서 $\mathcal{D}$는 많은 에피소드를 포함한 meta-trajectory이다. 우리는 $\mathcal{D}$에 하위 인덱스를 붙여 개별 trajectory들을 구분해서 사용한다. 일부 meta-RL 알고리즘은 $f_\theta$를 통해 $\mathcal{D}$를 $\phi$에 모든 MDP step에 매핑하고, 다른 알고리즘들은 이 매핑을 보다 덜 빈번하게 수행한다.
Meta-RL objective 표준 RL에서는 Markov policy만으로 목적 함수를 최대화하는 것이 충분하다. 반면, meta-RL에서는 inner-loop자체가 meta-trajectory를 입력으로 받아 policy 파라미터를 출력하는 전체 RL 알고리즘이다. meta-RL 알고리즘의 성능은 inner-loop가 task 분포로부터 샘플링 된 task $M$에 대해 수행하는 trial 중 생성한 정책 $\pi_\phi$가 달성한 보상을 기준으로 평가된다.
사용되는 응용 분야에 따라 다른 목적 함수가 사용된다. 어떤 응용에서는 탐색 또는 적응 기간을 허용할 수 있다. 이 경우 기간 동안 inner-loop가 생성한 정책의 성능은 중요하지 않고 최종적으로 찾은 정책이 task를 잘 해결하기만 하면 된다. 이때의 에피소드들은 inner-loop가 자유롭게 환경을 탐색할 수 있는 학습 기회로 사용된다.
다른 응용에서는 자유로운 탐색 기간이 허용되지 않으며 에이전트는 환경과의 상호작용이 시작되는 첫 순간부터 기대 보상을 최대화해야 한다. 어떤 목적을 최적화하느냐에 따라 학습되는 탐색 전략이 달라지며 자유 탐색 기간이 있는 경우에는 더 많은 위험을 감수하는 전략이 나타날 수 있다. 두 설정 모두에 적용 가능한 목적 함수는 아래와 같다:
$$\mathcal{J}(\theta) = \mathbb{E}_{\mathcal{M}^i\sim p(\mathcal{M})}\left[\mathbb{E}_\mathcal{D}\left[\sum_{\tau \in \mathcal{D}_{K : H}}G(\tau)\middle| f_\theta, \mathcal{M}^i\right]\right]$$
- $G(\tau) = \Sigma^T_{t=0}\gamma^t r_t$ : MDP $\mathcal{M}^i$의 trajectory $\tau$에서 총 보상 값
- $H$ : trial의 길이 혹은 task-horizon
- $K : H$ : trajectory의 인덱스가 $K$ 이상인 에피소드들로 구성
- $K$ : 첫 번째로 return이 목적 함수에 포함되는 에피소드의 인덱스. 일명 shot이라고 부름, 자유로운 탐색을 멈추는 인덱스 번호
만약 $K = 0$이라면 자유 탐색 기간이 없다는 것을 의미한다. 에피소드 $\tau$는 MDP $\mathcal{M}^i$에서 policy $\pi_\phi$를 이용해 샘플링되며 이때 정책의 파라미터 $\phi$는 inner-loop의 함수 $f_\theta(\mathcal{D})$에서 생성된다.
위의 식에서 정의된 meta-RL의 목적 함수는 task 분포 $p(\mathcal{M})$에서 샘플링된 task들에 대한 기댓값으로 평가된다. meta 훈련 중에는 실제 분포 $p(\mathcal{M})$를 정확히 알 수 없다는 가정 하에 해당 분포로부터 샘플링된 task들만을 사용하여 학습이 이뤄진다. 이로 인해 meta-testing 시점에는 학습 중 사용된 task들과는 새로운 task들이 등장할 수 있으며 이는 일반화 문제로 이어진다. 이 문제는 meta 테스트 작업 분포가 훈련 분포와 공유하지 않을 때 더 악화된다. 이런 out-of-distribution문제는 meta-RL 분야에서 중요한 연구 주제로 다뤄지고 있다.
POMDP Formalization
위의 식에서 정의된 meta-RL 문제 설정은 partially observable Markov decision process라는 특수한 형태로 간주할 수도 있다. POMDP는 튜플 $\mathcal{P} = \langle \mathcal{S}, \mathcal{A},\Omega ,P, P_0, R, O, \gamma \rangle$로 나타낼 수 있다.
- $\Omega$ : 관찰의 집합
- $O$ : 관찰 함수
- 나머지 : MDP랑 동일
우리는 위 첨자를 이용하여 함수가 MDP인지 POMDP인지 나타낸다. 예를 들어 POMDP의 보상함수는 $R^\mathcal{P}$로 나타낸다. POMDP의 핵심적인 차이점은 agent가 현재 state를 직접 관찰할 수 없고 대신 agent가 observation $o_t \in \Omega$를 $O(o_t \mid s_t^\mathcal{P}, a_t)$를 통해 직접 관찰한다. 따라서 POMDP policy는 과거의 관찰 이력에 기반하여 action 확률을 출력하는 함수가 된다.
MDP의 분포가 주어졌을 때 meta-RL 문제에 대응되는 POMDP는 특정한 구조를 가진다. POMDP는 숨겨진 상태 안에 MDP의 정체성을 함께 포함한다. POMDP의 상태는 $s_t^\mathcal{P} = (\mathcal{M}^i, s_t)$로 정의된다. POMDP의 관찰 함수는 현재 MDP의 state를 반환하며 과거의 action과 reward를 같이 반환한다: $o_t = (s_t,a_{t-1}, r_{t-1})$.
meta-RL에서는 MDP의 정체성이 agent에게 주어지지 않기 때문에 agent가 task-specific한 최적의 정책을 학습하기 위해서는 보상 함수에 대한 정보도 관찰을 통해 추론해야 한다. 이 때문에 일반적인 POMDP와 달리 관찰은 샘플링된 보상 $r_{t-1}$을 포함해야 한다. 이런 관찰의 시퀀스는 데이터셋 $\mathcal{D}$를 구성하여 inner-loop가 정책을 학습하는 것을 돕는다.
POMDP의 보상과 dynamics 함수는 샘플링된 MDP가 hidden state에 숨기고 있던 것을 그대로 사용한다. 추가로 샘플링된 MDP의 에피소드가 종료되었다면, POMDP의 dynamics 함수는 초기 상태 $P_0$에서 새로운 상태를 샘플링하여 다음 에피소드를 이어가도록 설계되어야 한다. POMDP의 한 에피소드는 샘플링된 하나의 MDP에 대해 수행되는 전체 trial로 구성된다. task-horizon $H$에 도달했을 때 POMDP는 끝나며 새로운 MDP가 다음 POMDP 에피소드에서 샘플링되며 시작된다. 이런 관점은 meta-RL 문제에 대한 아래의 통찰을 가져왔다.
첫 번째, POMDP의 이론에 따르면 최적의 policy는 관찰 이력에 의존하거나 숨겨진 state에 대한 충분한 통계에 의존하는 것으로 알려져 있다. 만약 inner-loop인 $f_\theta$가 관찰 이력의 일반적인 함수를 근사한다면 inner-loop $f_\theta$와 policy $\pi_{\theta,\phi}$는 하나의 통합된 객체로 간주될 수 있으며 이는 history-dependent policy, 즉, 이력 기반 정책으로 볼 수 있다. 이런 이력 기반 policy들은 meta-RL의 특정 구조를 범용적인 POMDP 이상으로 구체적으로 활용하지는 않지만, meta-RL 문제를 해결하는 데에는 충분하다.
반면 inner-loop가 POMDP의 숨겨진 state의 posterior 또는 belief state를 근사하는 방식이라면 $f_\theta$와 $\pi_{\theta, \phi}$의 조합은 belief에 기반한 policy로 해석될 수 있다. meta-RL에서는 숨겨진 state가 현재 주어진 task(MDP)라는 명확한 구조를 가지기 때문에, 이 belief state를 구성하는 충분한 통계 역시 일반적인 POMDP보다 더 구체적으로 정의 가능하다. 특히 하나의 충분한 통계는 작업을 통한 posterior 분포이며 뒤에서 더 다룰 예정이다. 이런 역사 의존적과 믿음 의존적의 이분법은 두 가지의 meta-RL 방법을 이끌어낸다. 하나는 black box 방법이고 다른 하나는 작업 추론 방법이다.
두 번째, 이런 관점은 Bayesian RL과의 연결점을 만들 수 있다. Bayesian RL은 작업에 대한 posterior 분포를 명시적으로 유지하고 이를 Bayesian 추론을 통해 업데이트함으로써 POMDP 문제를 해결한다. Bayesian 프레임워크는 사전 지식을 통합하는 편리한 방법을 제공해주며 명시적으로 불확실함을 유지하는데 유용하다. 이런 프레임워크를 사용하여 새로운 MDP를 구축할 수 있고 여기서 MDP는 Bayesadaptive Markov decision process (BAMDP)로 정의된다.
posterior를 state의 일부로 간주하므로 Markov policy를 사용할 수 있고 이로 인해 meta-RL 문제를 Markov 구조 안에서 해결할 수 있으며 탐색과 적응을 동시에 최적화할 수 있게 된다. BAMDP와 Bayes-최적화 policy는 아래에서 더 자세히 설명할 예정이다. Bayesian RL 방법은 반드시 명시적으로 모델을 설정하고 MDP의 분포를 업데이트해야 하기 때문에 실제로는 단순한 도메인에서만 계산 가능하다.
예를 들어 확장 가능한 Bayesian RL 방법이 이진 공간의 MDP에서만 가능한 경우가 많다. 대신 meta-RL 방법은 Bayesian posterior를 명시적으로 근사하지 않고 필요한 구성요소들을 학습을 통해 암묵적으로 모델링 할 수 있다. 예를 들어, meta-RL은 사전 분포(prior)에 대한 명시적인 정의 없이, 단지 prior에서 샘플링된 task에 접근할 수 있으면 충분하다. meta-RL 에이전트는 이러한 샘플들을 통해 task 분포에 대한 추론 능력을 내재적으로 학습할 수 있다.
세 번째, Meta-RL이 일반적으로 MDP를 통한 분포를 고려하지만 POMDP들의 분포를 고려하는 것도 가능하다. 이 경우 task 자체가 부분적으로 관찰 가능한 환경이 된다. 이런 설정은 meta-POMDP라고 불리는 또 다른 형태의 POMDP를 형성한다. meta-POMDP는 trial 동안 숨겨진 state의 일부만 고정되고 나머지는 에피소드 내에서 계속 변화하는 POMDP로 정의할 수 있다. 이런 구조에 맞춰 기존 meta-RL 방법들을 적절히 확장하거나 조정하여 적용하는 것도 가능하다.
Example algorithms
우리는 meta-RL 목적 함수를 최적화하는 두 가지 대표적인 meta-RL 알고리즘을 소개할 것이다. meta-gradients를 사용하는 Model-Agnostic Meta-Learning(MAML)과 관찰 이력에 의존하는 policy구조를 사용하는 Fast RL bia Slow RL(RL^2)이다. 많은 meta-RL 알고리즘은 MAML과 RL^2에서 사용된 개념과 기법들을 기반으로 발전되어 왔으며, 이 두 알고리즘은 meta-RL을 이해하기 위한 훌륭한 출발점이 된다.
MAML 많은 inner-loop 알고리즘 $f_\theta$는 기존 RL 알고리즘을 기반으로 하며 메타 학습을 사용해 개선하는 구조를 따른다. MAML은 이런 패턴을 따르는 영향력있는 디자인이다. MAML의 inner-loop는 메타-parameter $\phi_0 = \theta$를 초기 parameter로 사용하는 policy gradient algorithm이다. 핵심 통찰은 inner-loop가 초기 파라미터에 대해 미분 가능한 함수이므로 해당 초기값 $\phi_0$를 gradient descent를 통해 최적화 되어 좋은 시작 점을 설정할 수 있다. 새로운 작업에 적응할 때 MAML은 초기 policy에서 데이터를 수집하고 파라미터의 집합을 policy gradient를 적용하여 업데이트한다.
$$\phi^i_1 = f(\mathcal{D}^i_0, \phi_0) = \phi_0 + \alpha\triangledown_{\phi_0}\hat{J}(\mathcal{D}^i_0, \pi_{\phi_0})$$
- $\hat{J}(\mathcal{D}^i_0, \pi_{\phi_0})$ : 작업 $\mathcal{M}^I$에서 $\pi_{\phi_0}$을 이용하여 수집한 데이터 $\mathcal{D}^i_0$상에서 계산된 return의 추정값
- outer-loop에서 $\phi_0$을 업데이트하기 위해 policy $\pi_{\phi^i_1}$에서 수집한 데이터 $\mathcal{D}^i_1$을 이용하여 업데이트를 진행한다.
$$\phi'_0 = \phi_0 + \beta\triangledown_{\phi_0} \sum_{\mathcal{M}^i \sim p(\mathcal{M})}\hat{J}(\mathcal{D}^i_1, \pi^i_{\phi_1})$$
- $\pi^i_{\phi_1}$ : 작업 $i$가 inner-loop에 의해 업데이트된 policy
- $\beta$ : learning rate
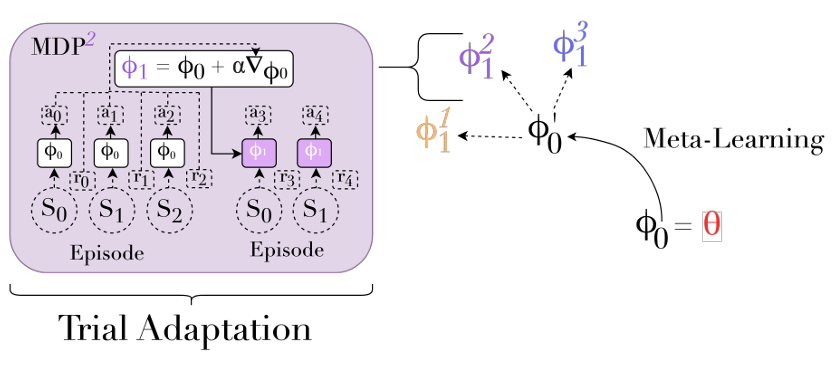
여기서 $\triangledown_{\phi_0}\hat{J}(\mathcal{D}^i_1, \pi_{\phi_1})$는 inner-loop를 통해 파라미터가 바뀐 policy의 성능이 초기 파라미터 $\phi_0$에 어떻게 의존하는지를 나타내며 meta-gradient라고 불린다. meta-gradient를 하강시키는 것은 outer-loop의 목적 함수를 최적화하는 것과 같다. 여기서 설명한 MAML의 구조는 inner-loop에서 한 번만 업데이트하는 버전을 기준으로 한다. 더 어려운 문제에서는 inner-loop가 여러번 업데이트될 수 있다. 이런 추가적인 업데이트는 meta-gradient의 정의나 계산 방식에는 영향을 주지 않는다. 알고리즘은 알고리즘 1과 그림 4에서 확인 가능하다.
일반적으로 MAML에서 shot $K$와 task-horizon $H$를 inner-loop에 의해 생성된 가장 최근의 policy의 성능만을 outer-loop에서 평가하도록 설정한다. 가장 단순한 경우, 한 개의 에피소드를 inner-loop를 업데이트하기 위해 사용한다면 $K = 1$, $H = 2$가 된다. inner-loop에서 여러번 업데이트를 하거나 각 policy에 대해 여러 epsiode를 샘플링하여 분산을 줄이고 싶을 경우 더 높은 값의 $K$와 $H$가 사용될 것이다.

$\textbf{RL}^2$ meta-RL에서 유명한 다른 방법은 inner-loop를 환경과의 상호작용 이력 전체에 의존하는 policy로 표현하고 task 분포로부터 샘플링된 여러 작업에 대해 end-to-end RL 방식으로 학습하는 것이다. 이 이력은 policy가 trial을 진행 중에 마주친 모든 states, actions, rewards을 포함한다. 이러한 방식은 환경에 대한 정보를 점점 더 수집하면서 행동을 적응시켜 나가는 policy를 학습하게 된다. 이것은 일반적인 POMDP 방법을 meta-RL에 적용하는 것과 같다. 비슷한 아이디어는 지도 학습에서 발견되는데 예시로 Hochreiter et al.가 있다. meta-RL에서는 Duan et al.과 Wang et al.이 제안한 $\textbf{RL}^2$방법이 이런 구조를 따른다. 여기서 이력에 의존하는 policy는 RNN으로 표시된다. 이 예제에서는 RNN에 초점을 맞추었지만 모든 이력 종속 정책이 사용 가능하다.
$\textbf{RL}^2$에서는 outer-loop의 목적 함수가 전체 trial에서 보상 합의 기댓값이다. 이것은 일반적인 강화학습에서 단일 에피소드의 return을 기준으로 하는 목표와 대조되며 복수의 에피소드를 포함하는 전체 trial 전체에 걸쳐 누적 보상을 고려한다. 위에서 정의했던 목적함수에서 $K = 0$으로 표현한 것과 유사하지만 discount 방식에는 차이가 있다.
$$\mathcal{J}_{RL^2}(\theta) = \mathbb{E}_{\mathcal{M}^i\sim p(\mathcal{M})}\left[\mathbb{E}_{\tau \sim p(\tau \mid \mathcal{M}^i,\theta)}\left[\sum_{t=0}^{HT}\gamma^t r_t \right]\right] $$
이 목적 함수를 최적화하기 위해 $\text{RL}^2$는 전체 trial을 하나의 연속적인 시퀀스로 처리하며 underlying MDP에서 여러 에피소드를 포함하더라도 RNN의 숨겨진 state는 중간에 초기화되지 않는다. 메타 파라미터 $\theta$는 RNN과 입력/출력을 처리하는 기타 neural network의 파라미터를 포함하고, task parameter $\phi$는 임시의 숨겨진 state이며 매 timestep마다 바뀐다. 해당 알고리즘은 알고리즘 2와 그림 5에서 확인이 가능하다.
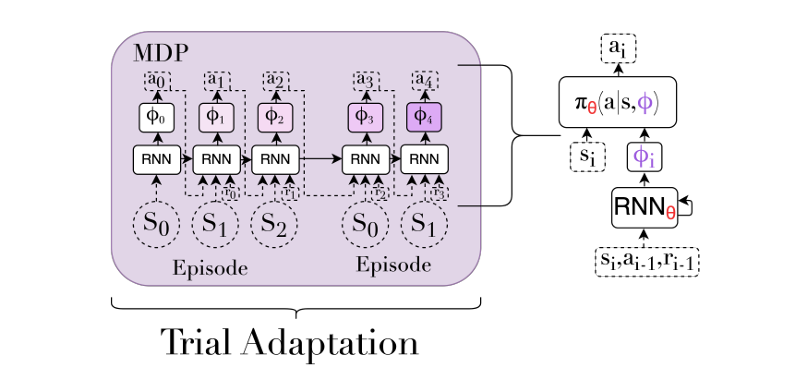

meta-RL에 대한 두 방식 MAML과 $\text{RL}^2$은 각자 장단점을 가지고 있다. 한편으로, MAML은 inner-loop에서 policy gradient 알고리즘을 사용하는 일반적인 구조를 기반으로 하며, 특정 조건 하에서는 초기 상태로부터 어떤 task에 대해서도 policy를 학습할 수 있는 유연성을 갖는다. 이에는 task 분포 밖에 있는 문제까지도 포함된다.
반면 $\text{RL}^2$은 직접적으로 meta-RL 목적함수의 최적화 policy를 근사화한다. 이 polic는 Bayes-optimal policy라고 불리며 해당 task 분포에 대해 가장 높은 기대 return을 제공하는 정책이다. Bayes-optimal policy는 항상 불확실한 MDP에서도 기대 보상을 최대화하는 action을 선택한다. 그러나 $\text{RL}^2$의 단점은 task 분포가 아닌 다른 task에서 학습을 진행할 때 일반화 문제가 발생한다는 것이다. end-to-end 학습 방식은 generalize한 policy를 배출하지 못한다.
Problem Categories
주어진 문제가 모든 meta-RL에 적용된지만, 문헌에서는 다음 두 가지 축을 기준으로 뚜렷한 클러스터들이 등장했다.
- task-horizon $H$가 짧은(few 에피소드)아 long(수백개 혹은 그 이상의 에피소드)인지
- task 분포 $p(\mathcal{M})$이 다양한 task를 포함하는지 아니면 하나의 task만 가지는지
이 두 기준을 조합하면 총 4가지 클러스터가 생성되며 이 중 세 가지가 실질적인 알고리즘으로 연결된다. 이러한 분류는 표 1에 정리되어 있으며 그 차이점은 그림 6에서 시각적으로 설명된다.
표 1에 나타난 첫 번째 클러스터는 few-shot multi-task setting이다. 이 설정에서는 agent가 task 분포에서 샘플링된 새로운 MDP에 대해, 단 몇 개의 episode만으로 빠르게 적응해야 하는 상황을 다룬다. 이러한 요구는 meta-RL의 핵심 아이디어를 반영한다. 즉, 다양한 task 분포에서 훈련된 agent가, 새로운 task에 대해서도 적은 환경 상호작용만으로 빠르게 학습할 수 있도록 만드는 것이다. 설정의 "shots"라는 용어는 few-shot classification 분야에서 유래된 것으로 모델이 소수 샘플만 보고 새로운 클래스를 인식하도록 훈련되는 구조와 유사하다. meta-RL에서 exploration 에피소드 $K$는 분류 문제에서의 shots와 유사한 역할을 하며 exploration과 adaption의 trade-off를 정의한다. 더 자세한건 다음 파트(few-shot)에서 다룬다.

few-shot 적응이 meta-RL에 대한 핵심 동기를 직접적으로 다루는 방식이지만 현실적으로는 agent가 소수의 에피소드만으로는 해결하기 어려운 적응 문제에 직면하는 경우도 존재한다. 예를 들어 작업 분포에 포함되지 않은 새로운 작업에 적응하는 상황에서는 기존의 경험만으로 빠르게 학습하는 것이 사실상 불가능할 수 있다. 이런 경우 inner-loop는 양질의 policy를 생성하기까지 수천 개 이상의 episode가 필요할 수 있다. 그럼에도 불구하고 우리는 meta-learning을 활용하여 inner-loop를 가능한 데이터 효율적으로 만들고 싶다. 이것을 우리는 many-shot Meta-RL 파트에서 더 자세히 다룰 것이다.
Meta-RL은 대부분 multi-task 환경에 초점을 맞추며 inner-loop는 task 간의 유사성을 활용해서 보다 데이터 효율적인 적응 과정을 학습할 수 있다. 일반적인 RL에서는 agent는 하나의 복잡한 작업에서만 훈련받는다. 이 방식은 데이터 효율성이 낮은 경우가 많이 때문에, 연구자들은 이것을 meta-learning과 결합하면 관련된 작업의 분포 없이도 효율성을 향상시킬 수 있다고 주장했다. 이런 경우 효율성의 향상은 agent의 단일 lifetime 내에서의 전이 또는 학습 과정에서의 국지적 조건에 대한 적응을 통해 이뤄져야 한다. 이런 경우 방법은 many-shot single-task로 불리며 이것 역시 many-shot Meta-RL 파트에서 다룰 것이다.
네 번째 클러스터는 few-shot single-task 설정으로 이 경우는 가상의 meta-learner가 단일 task에 대해, 단 몇 개의 episode만으로 학습을 가속화할 수 있다고 가정하는 환경이다. 하지만 agent의 lifetime이 매우 짧기 때문에, inner-loop가 데이터 효율적인 적응 절차를 학습하고, 이를 바탕으로 policy를 생성하기에는 시간이 충분하지 않다. 따라서 현재까지의 연구에 따르면, 이 설정을 직접적으로 겨냥한 실질적인 연구는 존재하지 않는다.
https://arxiv.org/abs/2301.08028
A Survey of Meta-Reinforcement Learning
While deep reinforcement learning (RL) has fueled multiple high-profile successes in machine learning, it is held back from more widespread adoption by its often poor data efficiency and the limited generality of the policies it produces. A promising appro
arxiv.org