이번 파트에서는 few-shot 적응 문제를 다룰 것이다. 이 설정에서는 agent가 다양한 task에 대해 meta-learning을 수행하고 meta-test 시점에서 새롭지만 유사한 task에 대해 몇 번의 에피소드만에 적응해야 한다.
하나의 예시로 전 글에서 다뤘던 로봇 요리사를 다시 가져와보자. 각 사용자의 집에서 새로운 요리 policy를 강화학습으로 처음부터 학습한다면 각 부엌에서의 많은 샘플을 요구할 것이며, 이는 요리에 대한 일반적인 지식은 공유될 수 있기에 비효율적이다. 특히 로봇이 고객의 부엌을 손상시킬 수 있는 행동을 하는 상황에서 데이터 낭비는 실질적으로 받아들일 수 없는 일일 수도 있다.
Meta-RL은 새로운 부엌의 차이점에 적응할 수 있는 절차를 데이터로부터 자동적으로 학습할 수 있다. meta 학습 동안 로봇은 시뮬레이션 환경이나 안전한 환경에서 다양한 형태의 부엌에서 훈련될 수 있다. 메타-testing 중에는 로봇이 손님에게 팔리고 새로운 부엌에서 일하며 빠르게 요리하는 법을 학습한다. meta-RL을 이용하여 agent를 학습하는 것은 도전 과제와 독특한 설계 선택를 동반한다.
특히 이 파트에서 우리는 다음 네 가지 기준으로 정리한다:
- inner-loop의 구조
- exploration 방식
- supervision의 유무 및 형태
- 강화학습 알고리즘이 model-based인지 model-free인지
쓰다보니 너무 길어서 4개의 파트로 또 분해해서 작성하기로 결정했다. 이번 파트는 exploration이다.
Exploration and Meta-Exploration
Exploration은 agent가 학습을 위해 데이터를 수집하는 과정이다.
- 표준 RL에서의 Exploration : 어떤 MDP에서도 작동해야 하며 무작위 탐색, 입실론-그리디, new state exploration 등으로 구성
- meta-RL에서의 Exploration
- outer-loop : 표준 RL과 유사한 탐색이 발생, meta-exploration이라고 부름
- inner-loop : 추가적으로 inner-loop exploration이 존재, 단순히 exploration이라고 부름
inner-loop에서의 exploration은 특정 task 분포 $p(\mathcal{M})$에 특화되어 있다. 샘플의 효율적인 적응을 위해 meta-RL agent는 task 분포에 대한 지식을 활용하여 효율적으로 탐색한다. 무작위 행동 대신 특정 정보를 얻기 위한 목표 지향적 exploration을 수행한다. 로봇 요리사의 예시를 또 들고오면 로봇 요리사가 찬장을 여는 행동이 이에 해당한다. 이런 exploration의 목적은 task 분포 내 MDP에 대한 few-shot adaptation에 필요한 정보가 풍부한 $\mathcal{D}$를 생성하는 것이다.
few-shot adaptation 설정에서는 agent가 new task에서 $K$개의 에피소드 동안 정보를 수집하고 적응한 후, 다음 $H - K$ 에피소드에서 task 해결 능력을 평가받는다. 그림 13에서 확인 가능하다. Agent는 처음 $K$개의 shot 동안 exploration을 진행하여 나중 에피소드에서 task를 잘 해결할 수 있도록 정보를 수집해야 한다. Agent는 new task에 대해 배우기 위한 exploration과 이미 알고 있는 것을 활용하는 exploitation 사이에서 균형을 맞춰야 한다.
여기서 최적의 exploration 전략은 다음과 같다.
- 처음 $K$ 에피소드 동안은 보상이 주어지지 않으므로 항상 exploration을 하는 것이 최적
- 이후 $H - K$ 에피소드 동안의 최적 exploration은 기간의 길이에 따라 달라진다:
- $H - K$가 길 때 : 단기 보상을 희생하더라도 exploration을 통해 더 나은 정책을 학습하여 나중에 더 큰 보상을 얻는 것이 유리하므로 더 많은 exploration이 최적
- $H - K$가 짧을 때 : 시간이 지나기 전에 최대한 보상을 얻어야 하므로 더 많은 exploiration이 필요
이 파트에서는 이런 trade-off를 다루는 다양한 접근 방식을 살펴볼 것이다.

End-to-end optimization
가장 간단한 방법은 end-to-end 방식을 활용하여 meta-RL 목표를 직접 최대화하는 것이다. 이런 방식은 meta-RL 목표를 최적화함으로써 최적의 탐색을 암묵적으로 학습할 수 있다. 후반 평가 에피소드에서 높은 보상을 얻기 위해서는 초기 에피소드에서 유용한 정보를 충분히 수집하는 탐색이 필수적이기 때문이다.
그러나 복잡한 탐색 전략이 필요한 task의 경우 이런 end-to-end 방식은 극도로 샘플 비효율적일 수 있다.
- 후반 에피소드에서 expolit를 잘 하려면 충분한 exploration이 필요함
- 그러나 exploration 전략 자체를 학습하려면 exploitation을 통해 얻어지는 보상이 필요함
- ex. 로봇은 재료를 모두 찾아야만 요리를 할 수 있지만 요리 결과로 보상을 받아야만 재료를 찾는 동기를 얻음
- 서로가 필요하기 때문에 end-to-end 방식은 복잡한 exploration이 필요한 task를 샘플 효율적으로 학습하는 데 어려움이 있다.
exploration이 end-to-end로 학습하면서도 성능을 개선하기 위해 추가 구성 요소를 도입한 연구들이 있다.
- E-RL2 : outer-loop 학습 시 초기 $K$ 에피소드의 모든 보상을 0으로 설정한다. 즉각적인 고밀도 보상에만 집중하여 필요한 exploration을 놓치는 것을 방지할 수 있다.
- 분리된 policy 학습 : PPG 방법 등에서는 exploration과 exploiration을 담당하는 분리된 policy를 학습하는 것이 유용할 수 있다. 이 경우 적응 초기에는 exploration을 선호하는 고정된 입십론 스케줄에 따라 행동 policy가 선택되며 exploration policy는 meta-learning되고 exploitation은 각 task마다 새로 학습된다.
복잡한 exploration 행동이 필요한 task 분포를 해결하기 위해 많은 방법들은 단순히 meta-RL 목표를 end-to-end로 최적화하는 것을 넘어 더 많은 구조를 추가하는 방향으로 발전하고 있다.
Posterior sampling
일부는 End-to-end 방식의 어려움을 해결하기 위해 posterior sampling을 통해 직접적으로 exploration하는 방법을 제안했다. 이는 Thompson sampling을 MDP에 확장한 개념이다. PEARL은 inner-loop에서 이 방식을 사용했고 알고리즘 3에서 확인이 가능하다.

작동하는 원리는 아래와 같다.
- Agent가 new task에 놓이면 task가 무엇인지에 대한 확률 분포를 유지하고 task와의 상호작용을 통해 이 분포를 반복적으로 개선하여 실제 task로 수렴하도록 함
- posterior sampling은 이 과정을 매 에피소드마다 현재 분포에서 task 정체성 $z$ 추정값을 하나 샘플링하고 해당 에피소드 동안은 샘플링된 $z$를 기반으로 task 정체성이 실제인 것처럼 policy를 행동하는 방식으로 수행
- 에피소드에서 얻은 observation은 task 분포를 업데이트하는 데 사용
- MDP task와 bandit task 모두에 적용 가능
그러나 아래와 같은 단점들이 존재한다.
- exploration과 exploitation에 동일한 policy를 사용하여 exploration 중에도 agent는 자신이 어떤 task에 있는지 알고 있는 것처럼 행동한다
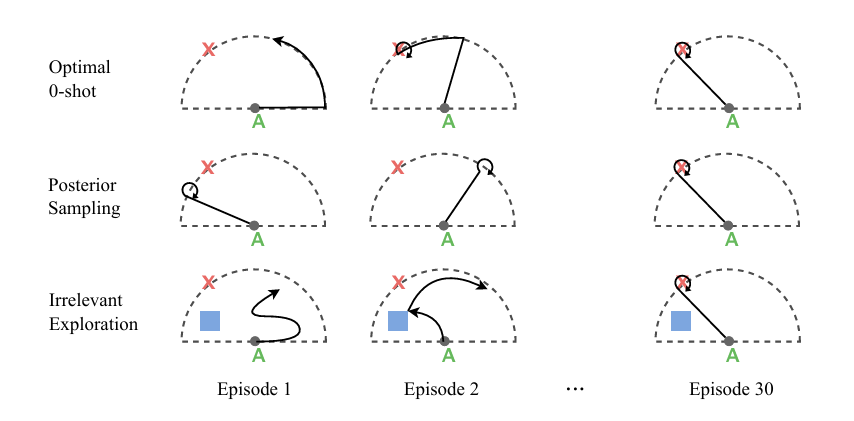
- 체계적인 exploration이 필요한 경우 비효율적일 수 있다(그림 14 참고)
Task inference
암묵적으로 exploration을 학습하는 방식(end-to-end 등)의 어려움을 피하기 위해 exploration을 장려하는 task inference 목표를 사용하여 agent가 탐색하는 방법을 직접적으로 학습시킬 수 있다. 이런 방법은 task 분포의 불확실성을 줄여주는 정보를 수집하도록 agent를 유도하는 intrinsic reward를 추가한다. 즉, task를 더 잘 예측(추론)할 수 있게 만드는 state들을 exploration하도록 정policy를 훈련한다. 결국 여기서 강조하는 것은 task를 정확히 파악하는 것이 최적의 policy를 학습하는데 필요하다는 것이다.
이런 접근 방식들 중 상당수는 exploration을 위한 policy와 exploitation을 위한 policy를 별도로 사용한다.
- $K$개의 few-shot처럼 exploration을 위한 별도의 에피소드가 주어질 때 흔함
- 학습 :
- 내재적 보상은 exploration policy를 학습할 때 사용.
- 표준 meta-RL 목표는 exploitation policy를 훈련할 때 사용
- 실행 :
- exploration policy가 먼저 $K$ 에피소드 동안 환경과 상호작용하며 데이터 수집
- exploitation policy는 exploration policy가 수집한 데이터를 바탕으로 나머지 $H-K$ 에피소드 동안 보상을 얻는 데 집중
이런 방식의 예시로는 DREAM이 있다.
- exploration이 유용한 정보만을 수집하도록 훈련
- $K$ shot이 너무 적을 때 특히 중요, task 해결에 무관한 정보 대신 필요한 정보에 집중하도록 만듬
- 순차적으로 훈련도 가능하지만 실제로는 안정성을 위해 동시에 훈련하는 경우가 많음
- DREAM의 구체적인 절차는 알고리즘 4와 5에서 확인 가능
- 단점 :
- 사전 task 정보가 존재하는 privileged information 설정을 전제로 함
- $K$ shot 내에서 필요한 정보를 얻는 것이 불가능할 때 성능이 떨어질 수 있음


Meta-exploration
표준 RL처럼 meta-RL에서도 outer-loop 학습, meta-training을 위한 데이터를 수집하는 과정이 필요하다. 이를 meta exploration이라고 부르며 inner-loop에서의 효과적인 exploration 전략을 학습하기 위한 데이터를 확보하는 과정이다. meta exploration은 outer-loop에서의 exploration으로 볼 수 있지만 inner-loop와 outer-loop가 데이터를 공유하기에 meta-exploration과 inner-loop exploration의 구분이 모호할 수 있다.
종종 outer-loop에서 표준 RL 알고리즘의 exploration(ex. 입실론-그리디)만으로 충분한 데이터가 수집되기도 한다. 그러나 meta-exploration을 명시적으로 개선하기 위해 많이 사용되는 방법은 intrinsic reward를 추가하는 것이다.
- 이전 문단처럼 task inference 보상의 경우도 meta-exploration으로 간주될 수 있다
- 그러나 task inference 보상만으로는 불충분할 경우가 있기에 다른 보상을 추가할 수 있다
- Novelty 보상 : Random Network Distillation(RND)와 같은 기법을 사용
- state와 task 표현의 결합 공간에서의 Novelty를 측정
- HyperX에서는 $r^\text{hyper}(\phi,s) = ||f(\phi,s)-h(\phi,s)||$의 novelty 보상을 사용
- 여기서 $f$는 예측 네트워크, $h$는 무작위 사전 네트워크이다.
- 오류 기반 보상 : TD-error와 같이 불확실하거나 학습이 잘 안 된 데이터를 얻도록 장려
HyperX에서는 아래와 같은 식을 사용하였다.
$$r^\text{error}(\phi,s) = -\log p_\theta(s'\mid s,a,\phi) - \log p_\theta(r\mid s,a,\phi)$$
$$\propto ||s' - \hat{s}'||^2_2 + ||r' - \hat{r}'||^2_2$$
이런 intrinsic 보상들은 학습 중에는 필요하지만 테스트 시에는 필요 없는 행동을 만들 수 있다. 또한 이런 추가 보상은 최적 policy 자체를 변화시킨다. 이런 문제를 해결하기 위해 아래와 같은 방법을 사용한다.
- 보상 점진적 감소 : intricsic 보상 부분을 점진적으로 줄여 실제 task 보상만을 최대화하도록 policy를 최적화
- Off-policy meta learning : meta-learning 자체를 off-policy 방식으로 수행, intrinsic 보상을 받는 데이터 수집 policy와 실제 task 성능을 위해 최적화되는 policy를 분리하여 훈련
Bayes-Adaptive Optimality
exploration에 대해 두 가지의 직관이 있다.
- 첫번째로, exploration은 현재 task의 dynamics 및 보상 함수에 대한 불확실성을 줄여준다.
- 모든 불확실성을 무작위로 줄이는 것은 최적이 아니다
- 예상되는 미래 보상을 증가시키는 '관련성 있는' 불확실성만 줄여야 한다
- 방해가 되거나 무관한 정보에 대한 불확실성을 줄일 필요가 없다
- 두번째로, exploration과 exploitation 사이에는 trade-off가 존재한다.
- 미래에 더 큰 보상을 얻기 위한 exploration은 당장의 exploitation을 희생해야 할 수 있다
- exploration 시간이 제한적일 때, task에 완전 적응하는 것 보단 일반적인 행동이 더 유리할 수 있다
이런 trade-off를 맞추기 위해 Bayes-adaptive Markov decision process(BAMDP)라는 특별한 유형의 MDP가 있다. 이 파트에서는 BAMDP에 대해 소개할 것이다. BAMDP의 솔루션은 exploration과 exploitation 사이에서 최적으로 균형을 맞추는 Bayes-optimal policy이다.
Bayes-adaptive Markov decision processes
BAMDP는 dynamics 및 보상 함수를 알지 못하는 MDP에 놓였을 때 policy가 얻을 예상 보상을 정량화하고 최적의 exploration-exploitation 균형을 찾는 policy를 결정하기 위한 프레임워크이다.
- BAMDP : 각 타임스텝에서 현재 agent가 가진 MDP에 대한 불확실성을 정량화
- 불확실성 하에서 예상되는 결과에 기반하여 다음 state와 보상을 모델링
- 보상을 최대화 하는 policy : 알려지지 않은 MDP에 놓였을 때 보상을 최대화하는 policy(Bayes-optimal policy)
BAMDP는 마르코프 속성을 만족시키기 위해 원래의 상태 $s_t$에 불확실성을 추가하여 state를 확장한다.
- BAMDP의 state : $s_t^+ = (s_t, b_t)$
- 원래 MDP의 state : $s_t$, 현재의 믿음 : $b_t$
- 믿음 $b_t = p(r,p\mid \tau_{:t})$은 현재까지 agent가 관찰한 궤적 $\tau_{:t} = (s_0, a_0, r_0, \dots, s_t)$와 일관되는 잠재적인 보상 함수 $r$ 및 전이 dynamics $p$에 대한 사후 확률 분포
- 초기 믿음 $b_0 : p(r,p)$
BAMDP의 보상 함수는 현재 믿음 $b_t$ 하에서의 예상 보상이다.
$$R^+(s_t,b_t,a_t) = \mathbb{E}_{R\sim b_t}[R(s_t,a_t)]$$
BAMDP의 transition dynamics도 유사하게 작동한다. 다음 state $s_{t+1}$ 및 다음 믿음 $b_{t+1}$로의 transition 확률은 현재 믿음 $b_t$하의 예상 전이 확률과 기저 MDP로부터 실제로 얻은 다음 state 및 보상에 기반한 베이즈 규칙에 따른 믿음 업데이트로 결정된다.
$$P^+(s_{t+1}, b_{t+1}\mid s_t,b_t,a_t) = \mathbb{E}_{R,P\sim b_t}[P(s_{t+1}\mid s_t,a_t)\delta(b_{t+1} = p(R,P\mid \tau_{:t+1}))]$$
즉, BAMDP는 알려지지 않은 기저 MDP와 상호작용하며 현재 불확실성을 지속적으로 업데이트 하는 과정이다. BAMDP의 표준 목표는 시간 범위 $H$ 동안의 예상 BAMDP 보상의 합을 최대화하는 것이다.
$$\mathcal{J}(\pi) = \mathbb{E}_{b_0,\pi}\left[\sum_{t=0}^{H-1}R^+(s_t,b_t,a_t)\right]$$
- $H$가 길수록 agent는 더 높은 보상을 찾을 시간이 많아지므로 explore하도록 장려
- BAMDP의 목표 함수는 표준 meta-RL 목표와 정확히 일치(이때 few-shot $K$는 0으로 설정)
Learning an approximate Bayes-optimal policy
그러나 Bayes optimal policy를 직접 계산하는 것은 매우 어렵다. BAMDP의 state인 하이퍼 state가 믿음, 즉 dynamics 및 보상 함수에 대한 분포를 포함하기 때문이다. 이런 분포를 포함하는 하이퍼 state 공간에서 planning을 수행하는 것은 일반적으로 계산 불가능하다.
하지만 실제 문제들에서 근사적으로 Bayes-optimal policy를 학습하기 위한 방법들이 있다.
- 아래의 두 가지를 동시에 학습하는 것이 주요 아이디어이다.
- 첫째, 믿음을 근사하도록 학습
- 둘쨰, 근사된 믿음에 조건화된 policy를 학습하여 BAMDP 목표를 최대
- VariBAD에서는 variational inference을 사용하여 믿음을 근사
- 근사적인 믿음 $b_t$를 잠재 변수 $m$에 대한 분포 $b_t = p(m\mid \tau_{:t})$로 표현
- policy를 실행하여 얻은 trajectory $\tau = (s_0, a_0, r_0, \dots, s_H)$을 사용하여 잠재 변수 $m$과 그 분포를 학습
- 관찰된 dynamics의 우도를 ELBO를 최대화하여 학습
- $b_t = p(m\mid \tau_{:t})$에 조건화된 policy $\pi(a_t \mid s_t,b_t)$이 표준 RL 기법을 사용하여 보상을 최대화
Connections with other exploration methods
모든 meta-RL 탐색 방법이 Bayes adaption optimal policy를 학습하려는 것은 아니지만 BAMDP 프레임워크는 이 방법들이 어떻게 탐색하는지에 대한 유용한 분석적 관점을 제공할 수 있다.
1. black box meta-RL 분석
- RL2 같은 black box 알고리즘은 현재 상태 $s_t$뿐 아니라 전체 기록 $\tau_{:t}$에 조건화되는 순환 policy를 학습하고, 이 기록은 RNN을 통해 은닉 state $h_t$로 처리
- 이 기록 $\tau_{:t}$는 베이즈 적응 policy에 필요한 믿음 상태 $b_t = p(r,p\mid \tau_{:t})$를 계산하기에 충분한 정보를 가지고 있음
- 따라서 black box 알고리즘은 은닉 상태 $h_t$에 믿음 상태를 인코딩함으로써 Bayes adaption optimal policy를 학습할 잠재력이 존재함
- ex) VariBAD는 black box 알고리즘에 은닉 상태가 믿음 상태를 잘 예측하도록 장려하는 보조 손실을 추가
- 실질적인 한계 : End-to-end 최적화의 어려움 때문에 복잡한 exploration을 효율적으로 학습하는 데 어려움을 겪음
2. few-shot 설정 방법들 분석
- 지금까지 이야기한 많은 방법들은 few-shot을 다룬다. 이는 초기에 $K$ 에피소드를 exploration에 사용하고 이후 에피소드의 보상을 최대화하는 것이 목표이다.
- 이는 BAMDP 목표에서 초기 $K$ 에피소드의 보상을 0으로 설정하는 것과 유사
- exploration 시간 $K$의 양에 따라 BAMDP이 최적 policy는 상당히 다른 exploration 행동을 유도할 수 있음
- few-shot을 위해 설계된 방법들은 $K$개의 자유 exploration 에피소드 동안 믿음 상태의 불확실성을 줄여 task를 파악하고 그 후에는 정보를 활용하여 보상을 얻는다. 이는 exploration과 exploitation이 섞이는 0-shot과 대조
3. BAMDP/Bayes optimal 관점에서의 특정 방법들 분석
- PEARL : PEARL의 posterior 샘플링 탐색은 현재 task에 대한 posterior 분포, BAMDP의 믿음 상태와 동등한 것을 유지한다. 불확실성을 줄이기 위해 이 분포에서 샘플링하고 그에 맞춰 행동하며 관찰 결과로 분포를 업데이트하여 믿음 상태의 불확실성을 붕괴시킨다.
- DREAM : DREAM은 초기 $K$ 에피소드 동안 task 관련 정보만을 효율적으로 수집하는 탐색 정책을 학습하여, 믿음 상태를 최적 exploitation policy에 필요한 dynamics 및 보상 정보만을 포함하도록 붕괴시키는 것을 목표로 한다.
https://arxiv.org/abs/2301.08028
A Survey of Meta-Reinforcement Learning
While deep reinforcement learning (RL) has fueled multiple high-profile successes in machine learning, it is held back from more widespread adoption by its often poor data efficiency and the limited generality of the policies it produces. A promising appro
arxiv.org
'논문 > 논문 정리' 카테고리의 다른 글
| Meta-Reinforcement Learning: Few-Shot Meta-RL (part 4) (0) | 2025.04.22 |
|---|---|
| Meta-Reinforcement Learning: Few-Shot Meta-RL (part 3) (0) | 2025.04.21 |
| Meta-Reinforcement Learning: Few-Shot Meta-RL (part 1) (0) | 2025.04.18 |
| Meta-Reinforcement Learning - Intro (0) | 2025.04.16 |
| [논문 정리] Combining Induction and Transduction For Abstract Reasoning (0) | 2025.04.14 |