[AGI] ARC-AGI Without Pretraining(by Isaac Liao)

bengal3636 2025. 4. 7. 17:28

Before we begin...

이번에 정리할 내용은 Isaac Liao의 ARC-AGI 접근법이다. 그는 사전 학습(pretraining) 없이 문제를 해결했으며, 운 좋게도 그의 발표를 직접 들을 기회가 있었다. 다만 발표 내용을 한 번에 이해하긴 어려워서, 복습을 위해 그의 블로그를 참고해보려 한다.

https://iliao2345.github.io/blog_posts/arc_agi_without_pretraining/arc_agi_without_pretraining.html

ARC-AGI Without Pretraining

By Isaac Liao and Albert Gu In this blog post, we aim to answer a simple yet fundamental question: Can lossless information compression by itself produce intelligent behavior? The idea that efficient compression by itself lies at the heart of intelligence

iliao2345.github.io

핵심 질문 : 손실 없는 정보 압축만으로 지능적인 행동을 만들어낼 수 있을까?

지능을 효율적으로 압축하는 아이디어는 새로운 것이 아니다. see, e.g., Hernández-Orallo & Minaya-Collado, 1998; Mahoney, 1999; Hutter, 2005; Legg & Hutter, 2007같은 경우들이 존재했다. 우리는 이론적인 논의를 되풀이하기보다는 이 아이디어가 실제로 작동하는 것을 보여주는 것을 목표로 한다.

우리는 압축에 기반한 방법으로 ARC-AGI 챌린지에 도전했으며, ARC는 IQ 테스트같은 퍼즐로 이루어져 있다. 우리는 이를 CompressARC라고 이름을 붙였으며 아래의 조건을 따른다:

No pretraining : 모델은 무작위로 초기화된다
No dataset : 한 모델은 목표 ARC-AGI 퍼즐만들 위해 훈련되며 한 가지의 답변을 출력으로 내보낸다
No search : 대부분의 의미로 gradient descent

이러한 제약에도 CompressARC는 훈련 셋에서 34.75%, 테스트 셋에서 20%의 정답률을 달성했다. 또한 각 퍼즐의 과정은 RTX4070 환경에서 20분이 소요되었다. 우리가 알기로는 이것이 단일 퍼즐만을 학습 데이터로 사용하는 최초의 neural method 방식이다. CompressARC의 지능은 오직 압축에서 온다.

이는 기존의 대규모 사전학습 + 방대한 데이터라는 접근에 도전장을 던지며, 최소한의 입력으로부터 깊은 지능을 추출할 수 있는 미래를 제안한다.

What is ARC-AGI?

ARC-AGI는 2019년에 만들어진 artificial intellignece 벤치마크이다. 적은 수의 예시를 보고 추상화 규칙을 찾는 능력을 시험하기 위해 개발되었다. 데이터셋은 IQ 테스트처럼 보이고 각 퍼즐은 일종의 규칙을 찾아 적용하는 것을 요구한다.

ARC-AGI가 처음 나온 논문은 "On the measure of Intelligece"라는 논문이며 앞에서 정리한 적이 있다.

https://bengal3636.tistory.com/14

[AGI] 2주차 논문 - On the Measure of Intelligence

AGI 수업에서 2주차 내용에 관련된 Chollet의 논문이다. 수업을 듣기 전에 미리 읽어보고 내용을 정리해보고자 한다.Context and historyNeed for an actionable definition and measure of intelligenceAI 연구는 인간과 유

bengal3636.tistory.com

https://juanmirod.github.io/public/papers/arc-AGI_.pdf

아래는 1000개의 퍼즐 중 3개의 예시이다:

모든 퍼즐에는 숨겨진 규칙이 존재한다. 너는 입력-출력 쌍의 매핑 예시를 보고 숨겨진 규칙을 모른 체 2번의 시도가 주어진다. 만약 정답을 맞추면 1점을 획득하고 틀릴 경우 0점을 획득한다. 너는 출력 그리드의 크기를 마음대로 바꿀 수 있고 각 픽셀의 색깔도 마음대로 변경할 수 있다. 퍼즐은 사람은 쉽지만 기계는 어렵게 설계되었다. 사람은 평균적으로 76.2%의 해결률을 보였고 전문가의 경우 98.5%의 해결률을 보였다.

400개의 훈련 퍼즐은 다른 퍼즐보다 쉬우며 아래의 핵심 지식을 파악하는 데 도움을 준다:

Objectness : 객체는 지속되며 이유없이 사라지지 않는다. 객체는 다른 것과 상호작용이 가능하며 상황에 따라 할 수도 있고 하지 않을 수도 있다.
Goal-directedness : 몇몇 객체는 "에이전트"이다. 그들은 목적이 있고 목적을 달성하려고 노력한다.
Numbers & counting : 객체는 개수를 세거나 모양, 존재, 움직임 등으로 분류될 수 있다.
Basic geometry & topology : 객체는 사각형, 삼각형, 원 같이 모양을 가질 수 있고 반사, 회전, 이동, 결합, 반복 등이 나타날 수 있다.

Our Solution Method

우리는 손실 없는 정보 압축이 ARC-AGI를 푸는데 효과적인 프레임워크를 제공한다고 제안한다. 더 효율적인 압축은 더 정확한 정보를 제공할 것이다. ARC-AGI 문제를 해결하기 위해 우리는 불완전한 퍼즐을 완전하게 바꾸는 시스템을 구축했다. 압축을 풀면 어떤 해법으로든 퍼즐을 재현할 수 있는 압축 표현을 찾아내는 방식으로 말이다. 가장 큰 도전과제는 정답을 제공하지 않은 채 압축 표현을 얻어야 한다는 것이다.

CompressARC는 디코더로 neural network를 사용한다. 그러나 인코딩 알고리즘은 또 다른 네트워크가 아닌, 추론 시간 동안의 경사하강법(gradient descent) 알고리즘을 이용한다. 다시 말하면, 인코더를 실행시키는 것은 디코더의 파라미터를 최적화하고 퍼즐의 압축 표현을 만들기 위한 입력 분포를 조정하는 것이다. 최적화된 결과 파라미터들은 퍼즐과 정답을 함께 담고 있는 압축된 비트 표현이 되는 것이다.

표준 머신 러닝 과정에서 본 CompressARC:(압축 용어 없이 간단히)

우리는 추론 시간에 시작해 ARC-AGI에게 퍼즐을 풀 시간을 제공한다.
neural network $f$를 만들어 퍼즐의 세부정보를 디자인한다(예시의 개수, 관찰된 색깔들). neural network는 무작위로 초기화된 input $z \sim N(\mu, \Sigma)$를 받고, 출력으로 정답을 포함하여 모든 그리드의 픽셀 단위의 색상 로짓(per-pixel color logit)을 내보낸다. 중요한 것은 $f_\theta$는 데이터 증강에 등변하다(입력이 변하면 출력도 같이 변하되, 같은 방식으로 일관되게 변한다).
- input-output 쌍을 reordering(입력-출력 쌍의 순서 변경)
- color permutations(색상의 치환)
- spatial rotations/reflections.(공간적 회전 및 반사)
네트워크 가중치 $\theta$를 초기화하고 파라미터 $\mu$와 $\Sigma$를 $z$의 분포로 설정한다.
$\theta$, $\mu$, 그리고 $\Sigma$를 cross-entropy의 합(정답을 제외한 5개의 그리드)을 최소화하기 위해 조정한다. 또한 KL divergence 페널티를 통해 $N(\mu, \Sigma)$를 $N(0,1)$(정규 분포)에 가깝도록 유지한다.
정답 그리드는 $z$의 무작위성 때문에 생성 결과가 확률적이며, 훈련 과정에서 여러 번 생성되는 정답 후보 중 가장 자주 나타난 그리드를 최종 정답으로 선택한다.

지금까지만 보면 왜 이 방법이 압축을 보여주는지 알 수 없을 것이다. 나중에 우리가 어떤 방식으로 ARC-AGI를 압축을 시도했는지 확인할 수 있다. 우선 이 방법이 실제로 퍼즐을 어떻게 풀려고 시도했는지부터 살펴보자.

Watching the Network Learn : Color the Boxes

Human Solution :

우리는 먼저 입력이 상자로 나누어지고, 출력 이미지에는 상자들이 색칠된채로 남아있다는 사실을 알 수 있다. 그 후, 우리는 어떤 색상이 어느 상자에 들어가는지 파악하려고 한다. 먼저 코너는 항상 검은색임을 깨닫는다. 그리고 가운데는 항상 마젠타 색상인 것을 알게되고 빨강은 위, 파랑은 아래, 초록은 오른쪽, 노랑은 왼쪽임을 깨닫는다. 이 단계에서 우리는 입력 이미지를 복사하여 출력이미지에 붙여넣은 후 상자를 방향에 맞게 색칠한다.

CompressARC Solution :

50 steps of learning: CompressARC의 네트워크는, 입력에 하늘색 행이나 열이 존재할 경우, 정답 그리드에도 동일한 위치에 하늘색을 출력한다. 이는 퍼즐 내의 다른 모든 입력-출력 쌍에서도 같은 대응 관계가 존재한다는 사실을 네트워크가 파악했음을 보여준다. 그러나, 그 외의 출력 픽셀들이 어떤 색이어야 하는지는 네트워크가 확신하지 못한다. 그래서 그 부분에 대해서는 네트워크 출력의 지수이동평균(exponential moving average)을 보면, 하늘색이 아닌 픽셀들에는 대부분 비슷한 평균 색상이 반복적으로 할당되는 경향이 있다.
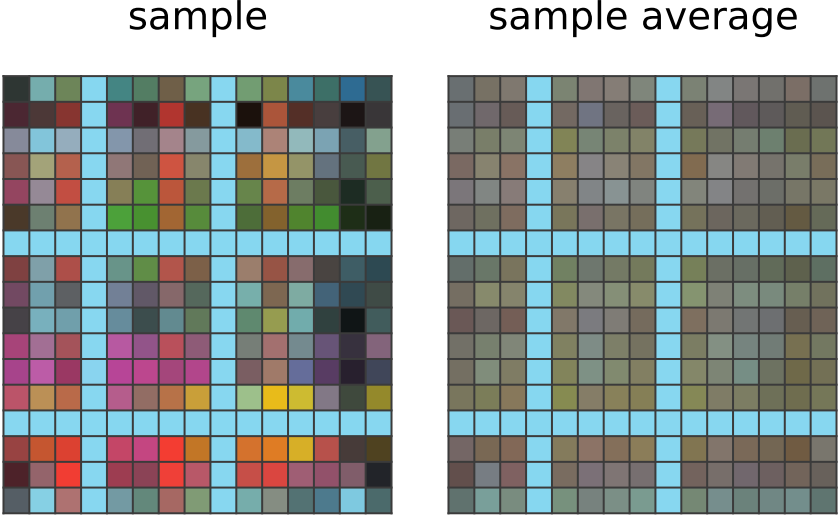150 steps of learning: 네트워크는 서로 가까이 있는 픽셀들이 비슷한 색상을 가지도록 정답 그리드를 출력한다. 이는 모든 입력-출력 예시에서 공통적으로 나타나는 특징이며,네트워크는 이러한 패턴이 정답 그리드에도 적용될 것이라고 추측한 것으로 보인다.
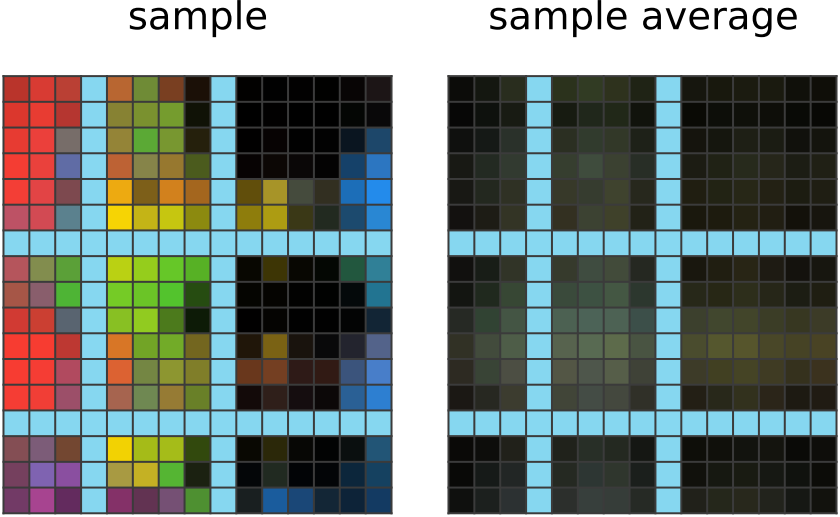200 steps of learning: 이제 네트워크의 결과에 하늘색 경계로 잘린 큰 색 덩어리들이 보인다. 이는 네트워크가 다른 예시 출력들에서 경계가 색상 블록을 나누는 데 사용된다는 점을 파악하고, 같은 방식을 정답에도 적용한 결과로 보인다. 또한, 다른 출력들에서 모서리 부분이 검은색 블록으로 채워져 있다는 점도 인식하여,이를 그대로 모방한 것으로 추측된다.
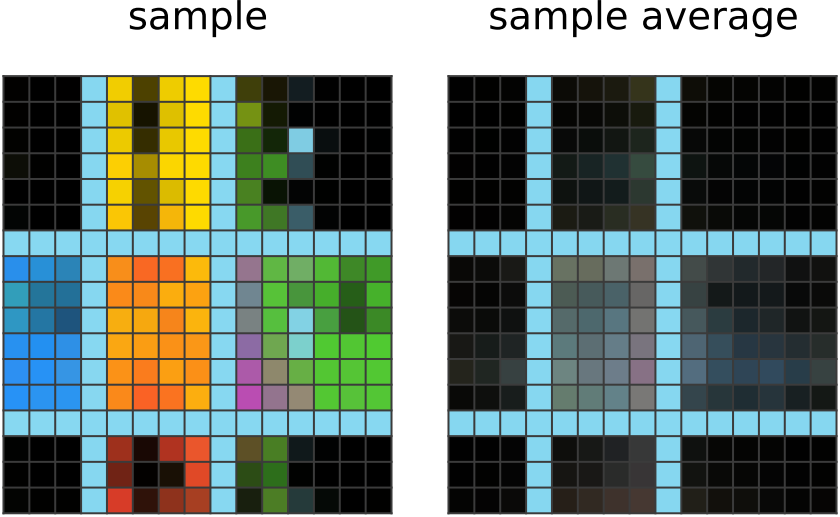350 steps of learning: 네트워크는 각 방향에 맞는 박스에 올바른 색상 부여를 성공적으로 한 결과를 보여준다. 단일 컬러를 방향 매핑에 사용한다는 사실을 파악하고 이를 모방한 것이다. 그러나 아직 어떤 색상이 정답인지는 헷갈려하는데 그 이유는 가운데는 방향이 없기 때문이다. 그럼에도 불과하고 평균 샘플의 경우 가운데에 올바른 색상인 마젠타가 보인다.
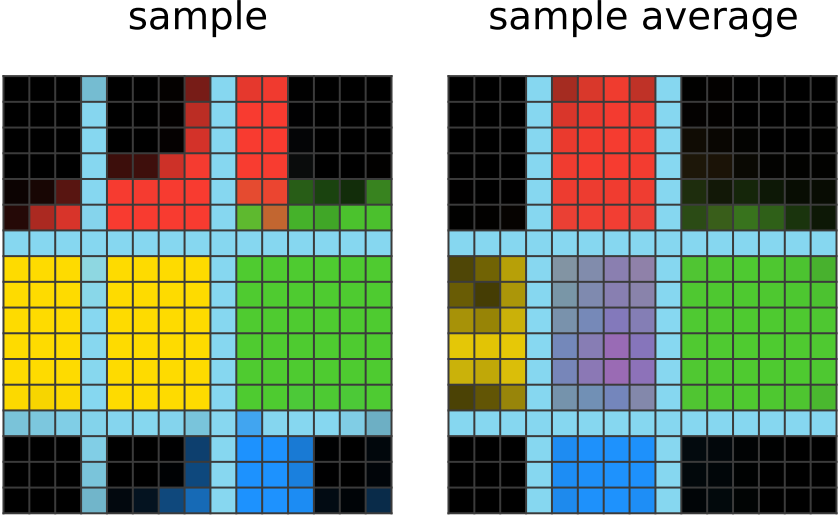1500 steps of learning: 이제 네트워크는 더 이상 개선되지 않을 만큼 충분히 정제된 상태이다. 가끔 출력된 샘플에서 실수를 할 때도 있지만, 그런 경우는 드물고 대부분 필터링되어 제거된다.

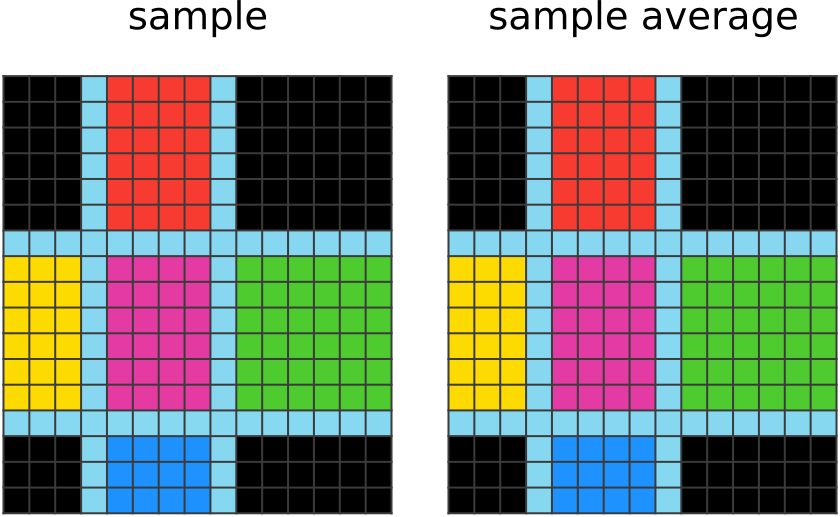학습이 끝난 후 z 분포를 분석해보면, 네트워크가 각 방향에 어떤 색을 대응시켜야 하는지, 그리고 행과 열을 어떻게 나눠야 하는지에 대한 정보를 그 안에 암묵적으로 '압축'해 두었음을 알 수 있다.

How to Derive our Solution Method

아직도 어떤식으로 압축이 되었는지 명확히 알 수 없다. 우리의 알고리즘을 도출하는 과정을 보면 정보 이론, 알고리즘 정보 이론, 코딩 이론을 우회하여 머신 러닝은 마지막에 등장한다.

A Primer on Lossless Information Compression

정보 이론에서 손실 없는 정보 압축은 어떤 정보를 가능한 가장 작은 비트로 표현하는 것이다. 그리고 그 정보를 다시 복원하는 것도 가능해야 한다. 이런 문제는 보통 아래와 같은 방식으로 추상화된다:

어떤 소스는 확률 분포 $p(x)$에 따라 symbol $x$를 생성하는 과정을 통해 symbol을 생성한다
인코더(encoder, $E$)는 이 symbol $x$를 비트 문자열 $s$로 변환한다
디코더(decoder, $D$)는 이 비트 문자열 $s$를 원래의 symbol $x$로 복원한다

목표는 $p$를 활용해서 어떠한 symbol도 틀리지 않고 비트 문자열 $s$의 기대 길이를 최소화하는 함수 $(E, D)$를 만드는 것이다.우리의 경우 symbol $x$는 ARC-AGI의 데이터셋(많은 퍼즐 + 정답 쌍)이고 우리는 가장 효율적으로 압축된 시스템이 정답을 어떻게 복원할지 알고 싶다. 문제는 우리가 정답을 $E$의 입력으로 제공받지 못하고 알지 못하고 확률 $p$, 즉 인간의 지능적 사고 과정을 수학적으로 모델링하기 어려으므로 알 수 없다. 이로 인해 이 문제는 훨씬 더 복잡해진다.

One-Size-Fits-All Compression

우리의 압축 구조를 만들기 위해 너는 아마 $p$를 알아야 한다고 생각할 것이다. 그러나 우리는 $p$가 상관 없다고 생각하는데 그 이유는 우리가 one-size-fits-all 압축기를 만들 수 있기 때문이다. 이는 이러한 가정을 전제로 한다:

$p$에서 샘플링된 ARC-AGI 데이터 세트 $x$에 대해 실질적으로 구현 가능하고 비트 효율이 높은 압축 시스템 $(E, D)$가 존재한다.

만약 이것이 틀렸다면 우리의 압축 아이디어는 무너질 것이다. 그렇기에 우리는 이러한 가정을 세웠다.

우리의 one-size-fits-all 압축기 $(E', D')$은 확률 $p$를 모른 상태로 만들어지만 오리지널 $(E, D)$ 만큼 비트-효율적이다:

$E'$은 symbol $x$를 관찰하고 프로그램 $f$와 입력 $s$를 고른 뒤 프로그램이 $f(s) = x$를 유지하는 조건에서 $\text{len}(f) + \text{len}(s)$를 최소화 한다. 이후 이 두 값을 쌍 $(f, s)$를 전송한다.
$D'$은 단순한 프로그램 실행기로 $f$를 $s$에 실행시키고 올바른 $x$를 생성하는 역할을 한다.

우리의 범용 압축기 $(E', D')$은 알고리즘 정보 이론을 이용하면 최선의 압축 효율에 매우 근접한다고 볼 수 있다. 그러나 문제점은 $E'$의 구현이 비현실적이라는 것이다.

왜냐하면 $E'$는 아래의 제약 조건 하에서 프로그램-입력 쌍 $(f, s)$의 길이를 최소화해야 하기 때문이다: $f(s)_{puzzle} = x_{puzzle}$. 즉, 출력의 퍼즐 부분은 입력 퍼즐과 같아야 한다는 조건을 만족해야 한다.

Neural Networks to the Rescue

프로그램 공간을 탐색하는 것을 피하기 위해 우리는 비트 효율성을 손해보더라도 단순히 프로그램 $f$를 고른다. 대신 프로그램의 다양성을 입력 $s$ 공간의 다양성으로 대체할 수 있기를 기대한다. 즉, 프로그램 $f$를 고정해두고 gradient descent를 통해 $s$를 탐색하는 것이다. 이때 $s$는 아래 세 가지로 구성된다:

$\theta$ : 신경망의 가중치
$z$ : 입력값
$\epsilon$ : 출력에 대한 수정값

프로그램을 바꾸는 대신 입력값을 조정하여 원하는 출력을 생성하는 방식을 선택한 것이다.

이런 제한된 압축 방식은 Relative Entropy Coding을 이용하여 노이즈한 가중치 $\theta$와 입력값 $z$를 각각 비트열 $s_\theta$와 $s_z$로 인코딩하고 출력 오차 보정값 $\epsilon$은 산술 부호화를 사용해 비트열 $s_\epsilon$으로 인코딩한다. 그 결과 $s$는 $(s_\theta, s_z, s_\epsilon)$으로 구성된다. 압축 방식은 아래와 같이 실행된다:

디코더는 $\theta = \text{REC-decode}(s_\theta)$, $z = \text{REC-decode}(s_z)$, $\text{logits} = \text{Neural-Net}(\theta, z)$, and $x = \text{Arithmetic-decode}(s_\epsilon, \text{logits})$의 순서로 실행된다.
인코더는 $\theta$와 $z$를 학습하여 코드 길이 $\mathbb{E}[\text{len}(s)]$를 최소화한다. $s_\epsilon$은 산술 부호화를 통해 올바르게 디코딩된다. 손실함수 $\mathbb{E}[\text{len}(s)]$를 계산하기 위해 우리는 REC의 특성을 활용한다:
- $\epsilon$은 코드 길이 $\mathbb{E}[\text{len}(s_\epsilon)]$이 총 crossentropy 오차와 동일하다.
- REC를 사용하기 위해 기존 분포 $q_\theta$를 고정하고 여기에 노이즈를 추가하여 $\theta$를 확률분포 $p_\theta$로 변환한다. 이때 REC는 노이즈가 섞인 $\theta$를 다음의 코드 길이로 저장할 수 있다고 보장한다: $\mathbb{E}[\text{len}(s_\theta)] = KL(p_\theta|| q_\theta) = \mathbb{E}_{\theta \sim p_\theta} [\log (p_\theta(\theta) / q_\theta(\theta))]$. 우리는 $q_\theta = N(0, I/2\lambda)$와 같은 정규 분포를 고정 분포로 선택하고 이 경우 손실은 $\mathbb{E}[\text{len}(s_\theta)] \approx \lambda | \theta|^2 + \text{const}$으로 근사되며 이는 디코더에 정규화를 적용하는 것과 동등하다.
- $z$ 또한 REC를 통해 인코딩되므로 같은 방식으로 처리한다. 기존 분포를 $q_z = N(0,I)$로 고정하면 다음과 같은 코드길이를 얻는다 : $\mathbb{E}[\text{len}(s_z)] = KL(p_z|| q_z) = \mathbb{E}_{z \sim p_z} [\log (p_z(z) / q_z(z))]$

내 나름대로 정리를 해보면 우선 $s$는 가중치 $\theta$, 입력값 $z$, 출력에 대한 수정 값 $\epsilon$으로 이루어진다. 우리의 목표는 입력 이미지 $x$가 $f(s) = x$를 만족하는 $s$를 찾는 것이다. 즉, $x$를 가장 짧게 압축하는 $s$를 찾는 것이다. 그 과정에서 $s$의 구성 요소인 파라미터들을 KL-divergence를 이용하여 학습한다(정규분포와 가까울 수록 압축하기 쉽기 때문에).

이 시점에서 앞에서 설명한 $s$의 전체 코드 길이가 VAE의 손실과 같다는 것을 깨달았을 것이다(= KL for $z$ + reconstruction error + regularization, VAE를 알고 있을 경우). 여기에 지금까지 설명한 등변성, 퍼즐 간 독립성, 정규화 항 생략 등을 더하면 CompressARC 모델의 설명을 얻을 수 있다.

Architecture

우리는 ARC-AGI 퍼즐을 풀기위해 우리만의 neural network를 만들었다. 이 네트워크는 잠재공간 $z$를 디코딩하는 역할이다. 가장 중요한 특징은 동등성이다. $z$가 변형되면 결과인 ARC-AGI 퍼즐 또한 똑같은 방식으로 변형되어야 한다:

input-output 쌍을 reordering(입력-출력 쌍의 순서 변경)
color permutations(색상의 치환)
spatial rotations/reflections.(공간적 회전 및 반사)

이러한 동등성 조건이 너무 많아 한 번에 다루기 어렵기 때문에, 우리는 먼저 완전히 대칭적인 구조를 기본으로 설계하고 필요에 따라 동등성을 깨는 계층들을 추가하여 원하는 방향성을 부여하는 방식으로 설계했다.

우리가 말한 것을 증명하기 위해 $z$와 ARC-AGI 퍼즐이 모두 다음과 같은 텐서 형태를 가진다고 가정해보자:

$$ [n\_examples, n\_colors, height, width, 2 \text{ for input/output}] $$

이때, 우리의 네트워크는 다음 차원들에 대한 인덱스 순열에 대해 동등한 성질을 갖도록 설계된다: $example$, $color$, $height$, and $width$ 차원. 즉, 입력 텐서에서 이들의 차원의 순서가 바뀌더라도 출력 또한 같은 방식으로 변형되어야 한다는 것이다.

실제 데이터($z$, 은닉 상태, 그리고 퍼즐)은 우리가 "multitensor"라고 부르는 것을 지나간다. 이것은 여러가지 모양과 크기를 가진 텐서들을 포함하고 있다. CompressARC에서 사용되는 모든 동등성은 멀티텐서를 변화시키면서 표현될 수 있다. 이것을 이해하기 위해서는 아래에 나올 "멀티텐서" 파트를 반드시 읽는 것이 좋을 것이다.

Multitensors

머신러닝의 대부분의 클래스들은 고정된 형태(rank)의 텐서를 사용한다. LLMs는 3 랭크 텐서인 $[n\_batch, n\_tokens, n\_channels]$,그리고 CNN은 4 랭크 텐서인 $[n\_batch, n\_channels, height, width]$의 형식을 사용한다. 우리의 멀티텐서는 여러 랭크를 가진 다양한 형태의 텐서들로 구성되어 있고 그들은 6 랭크의 텐서 $[n\_examples$, $n\_colors$, $n\_directions$, $height$, $width$, $n\_channels]$의 부분집합들로 표현된다. 우리는 항상 $channel$ 차원을 보존하며 그렇기에 이론적으로는 최대 32 텐서가 멀티텐서안에 들어갈 수 있다. 우리는 또한 일부 규칙을 적용하여 텐서 구조가 의미있는지 없는지에 따라 텐서의 수를 줄여 최종적으로 18개만 유지되도록 한다.

차원	크기
예시	ARC-AGI 퍼즐의 예시의 개수
색깔	ARC-AGI 퍼즐에서 사용하는 색깔, 검은색 제외
방향	8
높이	퍼즐 전처리시 결정
너비	퍼즐 전처리시 결정
채널	residual connection에서는 만약 $direction$ 차원이 포함되면 8, 아니면 16. 레이어 내부에서는 레이어에 따라 다름

멀티텐서가 데이터를 어떻게 저장하는지 감을 잡기 위해, 하나의 ARC-AGI 퍼즐을 $[examples, colors, height, width, channel]$ 형태의 텐서로 표현할 수 있다고 가정하자. 이때, $channel$차원은 input인지 output인지 구별하기 위해 사용되고 $width$/$height$는 픽셀의 위치를 나타낸다. 픽셀이 어떤 색상인지에 대한 정보는 $color$ 차원에서 one-hot 벡터로 표현한다. 비슷하게 $[examples, width, channel]$ 와 $[examples, height, channel]$ 텐서는 각 input/output에 대해 그리드의 형태를 나타내는 마스크를 저장하는 데 사용할 수 있다.

멀티텐서에 어떤 연산(operation)을 적용할 때, 우리는 기본적으로 $channel$ 차원을 제외한 모든 차원들은 동일하게 배치(batch) 차원으로 취급한다고 가정한다. 즉, 특별히 명시하지 않는 한, 해당 연산은 channel을 제외한 모든 차원의 인덱스들에 대해 복사되어 적용된다. 이러한 방식은 모델이 가지고 있는 대칭성(symmetry)을 유지하는 데 도움이 되며, 특정한 대칭을 깨뜨리기 위해 설계된 레이어를 사용할 때까지는 의도적으로 어떤 대칭도 깨지 않도록 해준다.

Results

Training set: 34.75%

Training Iteration	Time	Pass@1	Pass@2	Pass@5	Pass@10	Pass@100	Pass@1000
100	6 h	1%	2.25%	3.5%	4.75%	6.75%	6.75%
200	13 h	11.5%	14.25%	16.5%	18.25%	23.25%	23.5%
300	19 h	18.5%	21.25%	23.5%	26.75%	31.5%	32.5%
400	26 h	21%	25%	28.75%	31%	36%	37.5%
500	32 h	23%	27.5%	31.5%	33.5%	39.25%	40.75%
750	49 h	28%	30.5%	34%	36.25%	42.75%	44.5%
1000	65 h	28%	31.75%	35.5%	37.75%	43.75%	46.5%
1250	81 h	29%	32.25%	37%	39.25%	45.5%	49.25%
1500	97 h	29.5%	33%	38.25%	40.75%	46.75%	51.75%
2000	130 h	30.25%	34.75%	38.25%	41.5%	48.5%	52.75%

Evaluation set: 20%

Training Iteration	Time	Pass@1	Pass@2	Pass@5	Pass@10	Pass@100	Pass@1000
100	7 h	0.75%	1.25%	2.25%	2.5%	3%	3%
200	14 h	5%	6%	7%	7.75%	12%	12.25%
300	21 h	10%	10.75%	12.25%	13.25%	15.5%	16.25%
400	28 h	11.75%	13.75%	16%	17%	19.75%	20%
500	34 h	13.5%	15%	17.75%	19.25%	20.5%	21.5%
750	52 h	15.5%	17.75%	19.75%	21.5%	22.75%	25.5%
1000	69 h	16.75%	19.25%	21.75%	23%	26%	28.75%
1250	86 h	17%	20.75%	23%	24.5%	28.25%	30.75%
1500	103 h	18.25%	21.5%	24.25%	25.5%	29.5%	31.75%
2000	138 h	18.5%	20%	24.25%	26%	31.25%	33.75%

What Puzzles Can and Can't We Solve?

CompressARC는 자신이 할 수 있는 능력을 최대한 활용해 문제를 해결하려고 시도하지만 결국에는 어떤 한계점에 의해 막히게 된다.

예를 들어 퍼즐 28e73c20을 보면 모서리부터 시작해 중앙까지 가는 패턴을 확장해야 한다.

CompressARC의 네트워크에 포함된 레이어들의 특성상, 이 모델은 짧은 거리에서는 패턴을 잘 확장할 수 있지만 긴 거리에서는 확장이 어렵다. 그래서 CompressARC는 자신이 할 수 있는 최선을 다해 패턴을 짧은 범위까지는 정확히 확장한 뒤, 퍼즐의 중앙 근처에서는 정보가 부족하므로 추측에 의존하게 된다.

Case Study: Color the Boxes

위에서 봤던 퍼즐을 다시 보자.

학습을 진행할 때, reconstruction error는 매우 빠르게 감소했다. 전체적으로는 낮은 수준을 유지했지만 가끔씩 튀는 오차가 발생했고 그때마다 $z$로부터 KL발산도 함께 상승하는 경향을 보였다.

Solution Analysis: Color the Boxes

CompressARC가 어떻게 퍼즐을 풀까? $z$를 푸는 과정을 한 번 보자.

$z$는 멀티텐서이기 때문에, 각 텐서는 전체 KL 발산에 대해 기여하는 가중치를 가진다. 따라서 각 텐서가 얼마나 KL에 기여하는지를 살펴보면 어떤 텐서가 퍼즐을 표현하는 데 실제로 정보를 담고 있는지를 확인할 수 있다.

아래의 그래프는 디코딩 레이어에서 각 텐서 $z$가 얼마나 많은 정보를 담고 있는지, 즉 각 텐서의 KL 기여도를 시각화한 것이다.

학습이 진행되는 동안 대부분의 텐서들은 정보량이 0에 수렴한다. 즉, 무의미하다는 것이다. 하지만 딱 4개의 텐서만이 유의미한 정보를 유지하는 모습을 보인다. 물론 반복하다보면 이 4개 중 하나마저도 정보량이 0으로 떨어지는 경우가 있었고 CompressARC가 퍼즐의 정답을 제대로 복원하지 못하는 경우가 많았다.

위의 그림은 운이 좋았던 케이스로 $(color, direction, channel)$ 텐서가 정보량 0에 거의 도달했지만 200스텝쯤 다시 회복되었다. 흥미롭게도 그 지점에서부터 모델이 정확한 색을 정확한 박스에 넣기 시작했다.

$z$의 개별 텐서들이 디코딩 레이어에서 어떤 출력을 만들어내는지의 평균값을 관찰함으로써 그 텐서가 어떤 정보를 담고 있는지를 알 수 있다. 각 텐서에는 다양한 인덱스 조합마다 $n_channels$ 차원의 벡터가 들어있으며, 여기에 PCA를 적용해볼 경우 해당 텐서가 얼마나 많은 독립적인 정보 조각을 담고 있는지를 보여준다.

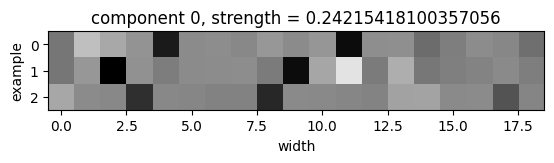
(Examples, height, channel) tensor : 예시에서 가장 밝게 나타나는 2개의 픽셀은 해당 퍼즐 그리드에서 하늘색 줄이 등장하는 행의 위치를 정확히 나타낸다.
(Examples, width, channel) tensor : 여기서는 가장 어두운 두 개의 픽셀이 그리드에서 하늘색 열이 위치한 열을 정확히 나타낸다.
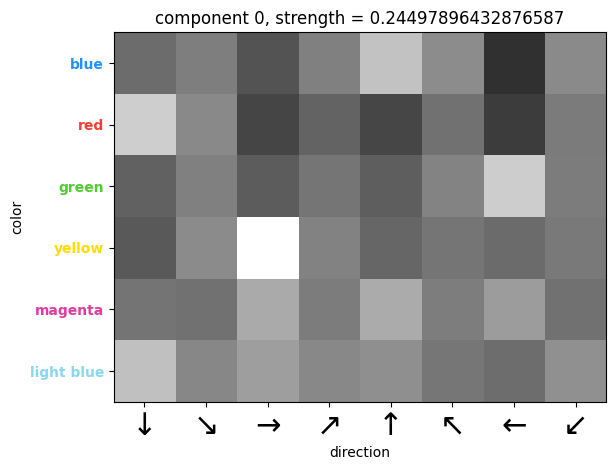
(Direction, color, channel) tensor : 이 텐서에서는 가장 밝은 4개의 픽셀이 다음과 같은 색상-방향 관계를 보여준다 : 파랑 = 위, 초록 = 왼쪽, 빨강 = 아래, 노랑 = 오른쪽. 즉, 이 텐서는 각 방햐에게 "반대 방향의 박스에 어떤 색을 써야 하는지"를 알려주는 역할을 한다.
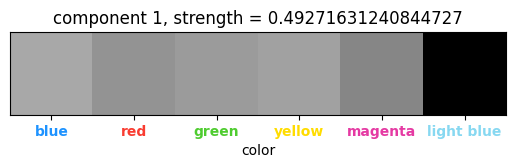
(Color, channel) tensor : 마젠타와 하늘색은 다른 색들과 명확히 구분되어 있는데 이는 퍼즐 상에서 마젠타가 중앙 박스를 표현하는 색, 하늘색이 행/열 구분선의 색으로 특수한 역할을 담당하고 있기 때문이다.

https://iliao2345.github.io/blog_posts/arc_agi_without_pretraining/arc_agi_without_pretraining.html

ARC-AGI Without Pretraining

iliao2345.github.io